Conservación del momento angular

¿Sabías que el derretimiento del hielo de los polos afecta ligeramente a la duración del día de la Tierra? En esta entrada vamos a entender por qué ocurre y, con ecuaciones de física básica, estimar cuánto cambiaría el día si todo el hielo Groenlandia se derritiera.

Hay más de una forma de definir el día. Para esta entrada voy a usar la del tiempo que tarda la Tierra en realizar una rotación completa respecto a su eje: 23 horas, 56 minutos y 4 segundos. Vayamos a lo que nos ocupa: ¿qué tiene que ver Groenlandia con todo esto?

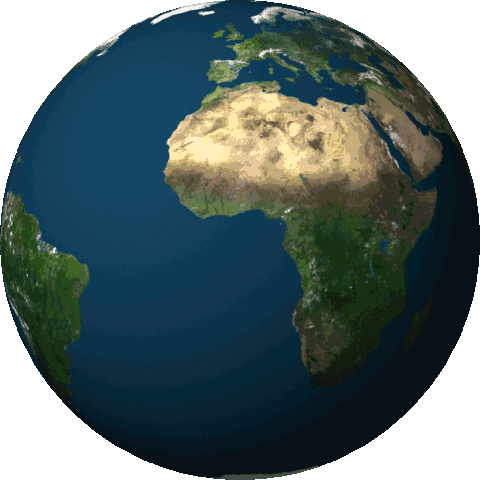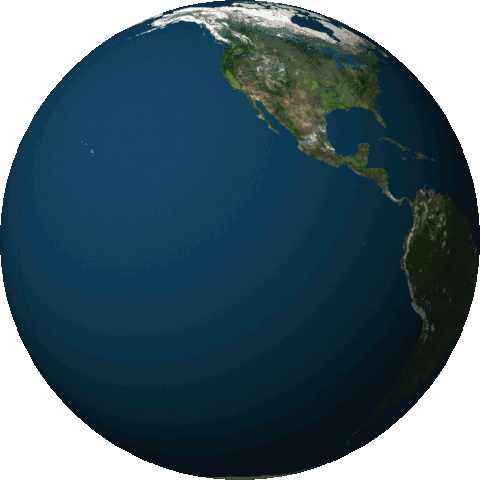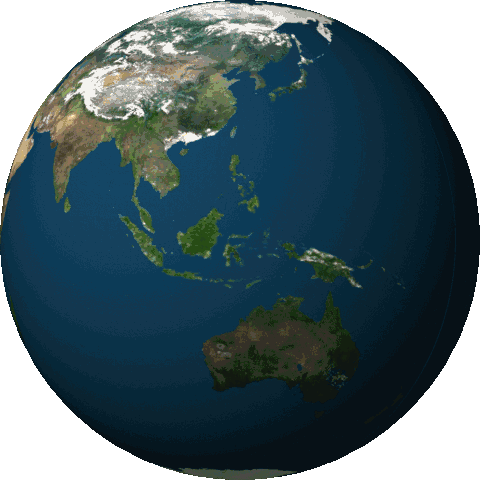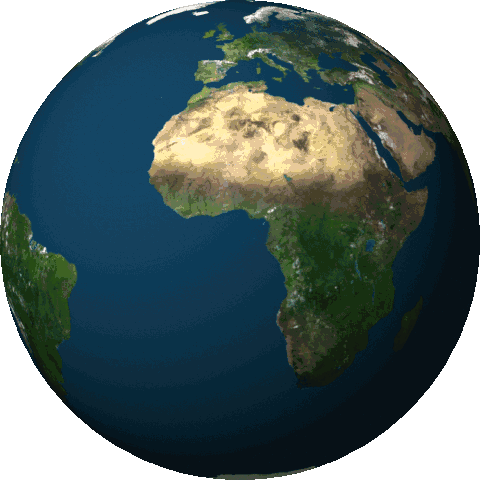
Groenlandia se encuentra prácticamente en el eje de rotación de la Tierra. Si el hielo de Groenlandia se distribuyera por el resto del planeta como agua, la velocidad de rotación de la Tierra caería.

Aunque no hayas estudiado Física, lo vas a entender con el patinaje. Fijaos en este gif. Al saltar, el patinador pega sus brazos al cuerpo para lograr una mayor velocidad y los separa para frenarse. En esta analogía, los brazos pegados es el hielo cerca del eje de rotación y el frenazo al separar los brazos es el agua distribuida por la Tierra.

Como veremos, el origen físico de esto es la conservación del momento angular. Hagamos números para ver si tenemos que añadir este tema como quebradero de cabeza relacionado con el cambio climático o si el efecto es demasiado pequeño para darnos cuenta. En rotación, el momento de inercia representa algo análogo a la masa en el movimiento rectilíneo. Es mayor cuanto mayor es la masa que rota, pero sobre todo aumenta cuanto más lejos se encuentra ésta del eje de rotación. Asumamos momento de inercia nulo para Groenlandia helada¹.

Por su parte, podemos tratar a la Tierra como una esfera enorme que rota sobre su eje. Asumiendo dicha forma esférica y distribución homogénea de la masa, obtenemos el siguiente valor del momento de inercia de la Tierra:

$$ I_\mathrm{T} = \frac{2}{5}M_\mathrm T R_\mathrm T^2 = 9.7\times 10^{37}\thinspace\mathrm{kg}\thinspace\mathrm{m^2} $$

Una vez el hielo se derrita, asumamos que el agua se distribuye homogéneamente por toda la superficie de la Tierra. Aplicamos la ecuación para una corona esférica cuyo radio interior es igual al radio exterior (aproximamos a un grosor infinitesimal):

$$ I_\mathrm{agua} = \frac{2}{3}M_\mathrm G R_\mathrm T^2 = 7.6\times 10^{31}\thinspace\mathrm{kg}\thinspace\mathrm{m^2} $$

Ese extra de momento de inercia es el que cambia la duración del día de la Tierra. Una de las leyes de conservación más famosas de la física es la del momento angular; para un objeto en rotación, el producto de su velocidad angular (lo rápido que rota) y su momento de inercia:

$$ \sum M_\mathrm{ext} = 0 \rightarrow \frac{\mathrm d L}{\mathrm d t} = 0 $$ $$ L = I\omega = I\cdot \frac{2\pi}{T} $$

Haciendo los cálculos, vemos que, para este modelo simplificado, la clave está en el cociente de masas. Como la masa del hielo de Groenlandia es un millón de veces menor que la del resto de la Tierra, el periodo de rotación, T, aumenta solo en una millonésima parte:

$$ I_1 = I_\mathrm T;\quad I_2 = I_\mathrm T + I_\mathrm{agua} $$ $$ \frac{I_2}{I_1} = 1 + \frac{\frac{2}{3}M_\mathrm G R_\mathrm T^2}{\frac{2}{5}M_\mathrm T R_\mathrm T^2} = 1 + 7.8\times 10^{-7} $$ $$ \frac{\mathrm d L}{\mathrm d t} = 0 \rightarrow \frac{T_2}{T_1} = 1 + 7.8\times 10^{-7} = 1.00000078 $$ $$ T_1 = 86164\thinspace\mathrm{s} \rightarrow T_2 = T_1 + 0.07\thinspace\mathrm s $$

Hemos obtenido que el día se alargaría 0.07 segundos. Haciendo cálculos mucho más exactos, la NASA obtiene un valor todavía inferior: 2 milisegundos, es decir, 0.002 segundos. Así que podemos quedarnos tranquilos en ese sentido; no nos daremos ni cuenta.

via GIPHY

De hecho, el día en la Tierra se ha estado lentamente alargando por la interacción de marea entre la Tierra y la Luna. A partir de los datos de civilizaciones antiguas sobre eclipses lunares, se estima que a un ritmo de unos 2 milisegundos cada 100 años². Es decir, si derretimos permanentemente el hielo de Groenlandia, habremos logrado un efecto similar en el periodo de rotación de la Tierra que la Luna en un siglo.

Lamentablemente, hay otros factores que sí nos deben preocupar respecto a la progresiva reducción del hielo en Groenlandia que estamos viviendo en nuestro planeta: desde el aumento del nivel del mar hasta cómo afecta a la fauna de ese ecosistema.

Finalmente, dejo una pregunta en el aire. Hemos visto que, al derretirse el hielo, el momento angular de nuestro planeta se conserva. Otra ley física de conservación bastante conocida es la de la energía. En este caso, ¿crees que la energía mecánica de un sistema en rotación cuyos elementos cambian su distancia respecto al eje de rotación, como el planteado en este artículo (o el del bailarín), se conserva?

El ejercicio de este hilo se planteó este año en mi facultad al alumnado de 1.° de Física para Ingeniería. La mayoría acertó, pero recuerdo que un estudiante respondió que el día aumentaría en 24 horas. ¡Vista la progresiva disminución del hielo en Groenlandia y en el resto de las zonas polares debido al cambio climático no sé cómo pudo dormir tranquilo esa noche!