La actividad científica
La investigación científica, magnitudes escalares y vectoriales, análisis dimensional, errores en la medida y expresión de resultados
 Foto de Hans Reniers en Unsplash
Foto de Hans Reniers en Unsplash
Índice
La investigación científica
La investigación científica es el proceso por el cual, mediante la aplicación del método científico, se consigue ampliar el conocimiento o dar solución a problemas científicos.
¿Sabes en qué consiste un doctorado o Ph.D. por sus siglas en inglés? Descúbrelo aquí
Imagina un círculo que contiene todo el conocimiento de la humanidad:

Cuando terminas el colegio, sabes un poquito:

Cuando terminas el instituto, sabes un poco más:
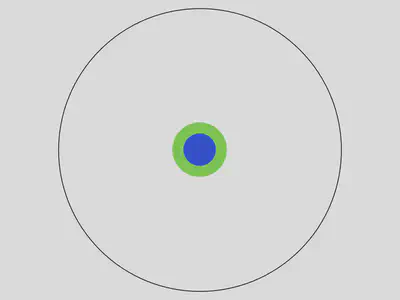
Cuando te gradúas en la universidad, consigues una especialidad:
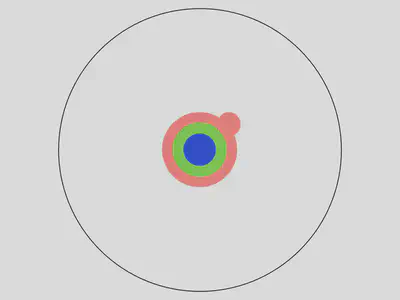
Con un máster profundizas en dicha especialidad:
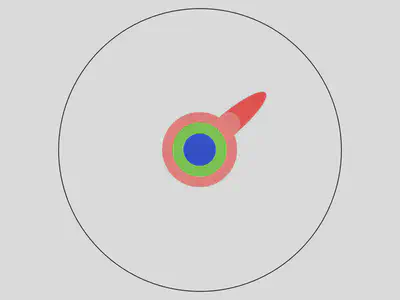
La lectura de literatura científica te lleva hasta la frontera del conocimiento de la humanidad:
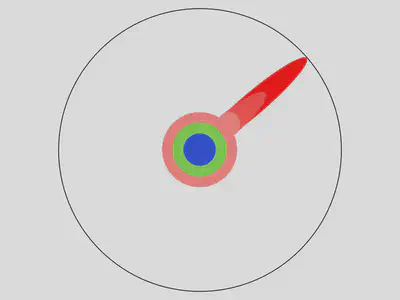
Una vez en el límite, te centras en un tema específico:
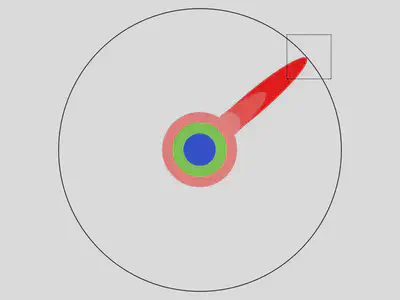
Empujas el límite durante unos años:

Hasta que, un día, el límite cede:

Y esa mella que has hecho se llama doctorado (Ph.D.):
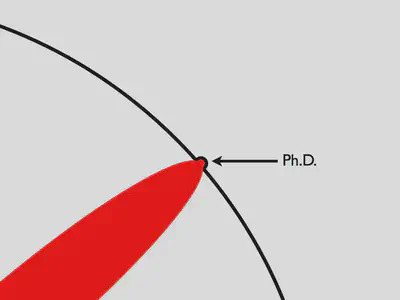
Por supuesto, el mundo te parece muy distinto ahora:

Pero no olvides tomar perspectiva:
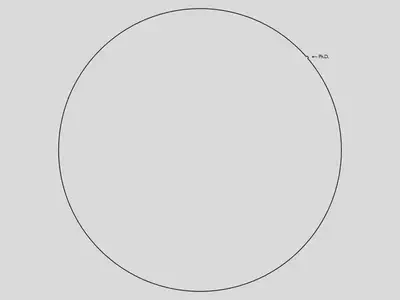
Sigue empujando.
Fuente: https://ictlogy.net/sociedadred/20100818-guia-ilustrada-para-un-doctorado/
Hipótesis, leyes y teorías
Hipótesis
Una hipótesis científica es una propuesta de explicación de un fenómeno, comprobable mediante el método científico.
Ley
Las leyes científicas son enunciados, basados en experimentos u observaciones repetidas, que describen o predicen una serie de fenómenos naturales.
Teoría
Una teoría científica es una explicación de un aspecto del mundo natural que puede ser repetidamente comprobado y verificado en condiciones controladas, de acuerdo con el método científico.
Magnitudes escalares y vectoriales
Magnitudes escalares
Son aquellas magnitudes que quedan descritas por un número (escalar) y una unidad.
Ejemplos
Masa, volumen, densidad, tiempo, temperatura, energía…
Magnitudes vectoriales
Son aquellas magnitudes que quedan descritas por:
- Un número (escalar).
- Una unidad.
- Una dirección.
- Un sentido.
- Un punto de aplicación.

Ejemplos
Posición, desplazamiento, velocidad, aceleración, fuerza…
Magnitudes básicas y derivadas
Magnitudes básicas del SI
El Sistema Internacional de Unidades (SI) define siete magnitudes básicas:
| Magnitud | Unidad | Símbolo |
|---|---|---|
| Tiempo | Segundo | s |
| Longitud | Metro | m |
| Masa | Kilogramo | kg |
| Corriente eléctrica | Amperio | A |
| Temperatura | Kelvin | K |
| Cantidad de sustancia | Mol | mol |
| Intensidad luminosa | Candela | cd |
El Sistema Internacional de Unidades (SI) sufrió una revisión en 2018. Puedes leer más sobre ello aquí.
Magnitudes derivadas
Las magnitudes derivadas se obtienen a partir de dos o más magnitudes básicas.
Ejemplos
Superficie, volumen, densidad, velocidad, aceleración, fuerza, presión, energía…
Análisis dimensional
El análisis dimensional nos permite relacionar las dimensiones (unidades) de una magnitud derivada con las de las magnitudes básicas en las que se basa.
Ecuación de dimensiones
Las ecuaciones de dimensiones son expresiones algebraicas en las que sustituimos las magnitudes físicas por sus dimensiones (unidades). Para denotar las dimensiones de una magnitud utilizamos la notación de corchetes $[\ ]$. Destacamos: \begin{align*} [\text{Masa}] &= \mathsf M \\ [\text{Longitud}] &= \mathsf L \\ [\text{Tiempo}] &= \mathsf T \end{align*} Siempre que trabajemos con ecuaciones de dimensiones trataremos de expresar las dimensiones de las magnitudes físicas que nos encontremos en función de $\mathsf M$, $\mathsf L$ y $\mathsf T$.
Ejemplos
$$ [S] = \mathsf{L}^2; [V] = \mathsf{L}^3; [d] = \mathsf{M}\mathsf{L}^{-3}; $$$$ [v] = \mathsf{L}\mathsf{T}^{-1}; [a] = \mathsf{L}\mathsf{T}^{-2}; [F] = \mathsf{M}\mathsf{L}\mathsf{T}^{-2} $$
Ejemplo resuelto
Demuestra que la energía cinética,
$$ E_\mathrm c = \frac{1}{2} m v^2, $$y la energía potencial gravitatoria,
$$ E_\mathrm p = mgh, $$tienen las mismas dimensiones, donde $m$ es masa, $v$ es velocidad, $g$ es la aceleración de la gravedad y $h$ es altura. Utiliza el resultado para definir la unidad de energía en el SI, el julio (J), en función de las unidades de masa, longitud y tiempo del SI.
Analizamos las dimensiones de la energía cinética $E_\mathrm c$:
$$ \left[E_\mathrm c\right] = \left[\frac{1}{2}mv^2\right] = \left[m\right]\cdot \left[v^2\right] = \mathsf{M}\cdot \left[v\right]^2, $$donde hemos utilizado que los números (escalares) no tienen dimensiones.
Necesitamos conocer las dimensiones de la velocidad:
$$ v = \frac{\Delta x}{\Delta t} \rightarrow \left[v\right] = \frac{\left[\Delta x\right]}{\left[\Delta t\right]} = \frac{\mathsf{L}}{\mathsf{T}} = \mathsf{L}\mathsf{T}^{-1} $$Por lo que llegamos a:
$$ \left[E_\mathrm c\right] = \mathsf{M}\left(\mathsf{L}\mathsf{T}^{-1}\right)^2 = \mathsf{M}\mathsf{L}^2\mathsf{T}^{-2} $$Analizamos ahora las dimensiones de la energía potencial gravitatoria $E_\mathrm p$:
$$ \begin{aligned} \left[E_\mathrm p\right] = \left[mgh\right] &= \left[m\right]\cdot \left[g\right]\cdot \left[h\right] \\\\ &= \mathsf{M}\cdot\left[g\right]\cdot\mathsf{L} \end{aligned} $$Necesitamos conocer las dimensiones de la aceleración $g$:
$$ \begin{aligned} g\equiv a = \frac{\Delta v}{\Delta t} \rightarrow \left[g\right] = \frac{\left[\Delta v\right]}{\left[\Delta t\right]} &= \frac{\mathsf{L}\mathsf{T}^{-1}}{\mathsf{T}} \\\\ &= \mathsf{L}\mathsf{T}^{-2} \end{aligned} $$Por lo que llegamos a:
$$ \left[E_\mathrm p\right] = \mathsf{M}\cdot\mathsf{L}\mathsf{T}^{-2}\cdot\mathsf{L} = \mathsf{M}\mathsf{L}^2\mathsf{T}^{-2} $$El julio (J) por lo tanto queda definido como:
$$ 1\thinspace\mathrm J = 1\thinspace\mathrm{kg}\thinspace\mathrm{m^2}\thinspace\mathrm{s^{-2}} $$Errores en la medida
Siempre que se realiza una medida experimental con un instrumento, esta lleva asociada una incertidumbre, que hace que sea imposible obtener dos medidas exactamente iguales. Los errores experimentales son la diferencia entre los valores medidos y los valores reales. Distinguimos entre errores sistemáticos y errores aleatorios.
Errores sistemáticos y errores aleatorios
Error sistemático
Siempre ocurre, con el mismo valor, cuando usamos el instrumento de la misma manera y en el mismo caso. Es predecible y típicamente constante o proporcional al valor verdadero. Suele ser debido a imperfecciones del instrumento de medida o de los métodos de observación (incluido el observador). Se puede detectar y eliminar.
Error aleatorio
Error inevitable que siempre está presente en cualquier medición. Causado por fluctuaciones inherentemente impredecibles. Se puede estimar comparando medidas y reducir promediando muchas medidas.
Precisión, veracidad y exactitud
Precisión
Es la cercanía entre los valores medidos obtenidos en mediciones repetidas bajo condiciones similares. Es una descripción de los errores aleatorios.
Veracidad
Es la cercanía entre la media de un número infinito de valores medidos repetidos y un valor de referencia. Es una descripción de los errores sistemáticos.
Exactitud
Es la cercanía entre un valor medido y el valor verdadero de la magnitud que se pretende medir.
Una alta exactitud es una combinación de alta precisión y alta veracidad.
.](/media/actividad-cientifica-4ESO/precision-veracidad-exactitud.svg)
Error absoluto y error relativo
Error absoluto
Es la diferencia entre el valor medido y el valor real:
$$ \text{error absoluto} = \lvert\text{valor medido} - \text{valor real}\rvert $$Tiene las mismas dimensiones que la magnitud medida.
Error relativo
Es el cociente entre el error absoluto y el valor real:
\begin{align*} \text{error relativo} &= \frac{\text{error absoluto}}{\text{valor real}} \\ &= \frac{\lvert\text{valor medido} - \text{valor real}\rvert}{\text{valor real}} \end{align*}
Es adimensional (suele expresarse en % multiplicándolo por 100).
Expresión de resultados
Por regla general, las incertidumbres siempre se expresan con una sola cifra significativa1, redondeando la medida en consecuencia (unidades, decenas, centenas, etc.).
Ejemplos
- $t = (5.67\pm 2.00)\thinspace\mathrm s \rightarrow t = (6\pm 2)\thinspace\mathrm s$
- $l = (1307\pm 202)\thinspace\mathrm{\mu m} \rightarrow l = (1300\pm 200)\thinspace\mathrm{\mu m}$
- $m = (437\pm 27)\thinspace\mathrm g \rightarrow m = (440\pm 30)\thinspace\mathrm g$
- $I = (17 \pm 3)\thinspace\mathrm{mA} \rightarrow \text{está bien expresada}$
-
Excepto cuando la primera cifra significativa es un 1, que entonces utilizamos dos. ↩︎
Participa activamente en la web comentando, dando tu opinión, realizando peticiones, sugerencias...
Discord