Estructura de la materia
- Modelos atómicos
- Orígenes de la teoría cuántica
- Mecánica cuántica
- Orbitales atómicos
- Estructura electrónica
- Partículas subatómicas
Descarga estas diapositivas en formato PDF 📥
Modelos atómicos
(continúa hacia abajo)
👇
Aprende más sobre John Dalton, J.J. Thomson, Ernest Rutherford y Niels Bohr echando un vistazo a sus biografías científicas en nuestra sección de Historia de la Ciencia.
Dalton
Basándose en las ideas de Demócrito, John Dalton propuso este modelo a principios del siglo XIX, considerando al átomo como una esfera maciza indivisible.

Los descubrimientos de la radiactividad natural por Becquerel (1896) y el electrón por Thomson (1897) hicieron necesaria la revisión de este modelo.
Thomson
También conocido como el modelo del pastel de pasas, fue propuesto en 1904 por J.J. Thomson, quien considera que el átomo está formado por una nube esférica con carga positiva en donde se encuentran incrustados los electrones, con carga negativa, como las pasas en un pastel.

Los descubrimientos del núcleo atómico y del protón por Rutherford (1911 y 1919, respectivamente) llevaron a la revisión de este modelo.
Rutherford
Gracias a su famoso experimento de la lámina de oro (Au), Ernest Rutherford propuso, en 1911, un modelo de átomo formado por un núcleo, muy pequeño comparado con el tamaño del átomo, con carga positiva y donde se concentra casi toda su masa. Los electrones, con carga negativa, giran alrededor del núcleo como lo hacen los planetas alrededor del Sol.

La integridad del núcleo y la inestabilidad de las órbitas electrónicas desde un punto de vista clásico hicieron necesaria la revisión de este modelo.
Bohr
Propuesto en 1913 por Niels Bohr para explicar la estabilidad de la materia y los característicos espectros de emisión y absorción de los gases.
Espectros atómicos
(continúa hacia abajo)
👇
Emisión
El espectro de emisión atómica de un elemento es único y está formado por un conjunto de líneas luminosas correspondientes a las ondas electromagnéticas emitidas por átomos de ese elemento, cuando se le comunica energía.
Una muestra gaseosa de átomos de un elemento contenidos en un tubo de vacío, se excita mediante una descarga eléctrica o calor. Cuando los átomos excitados de dicho elemento vuelven a su estado fundamental, emiten la energía absorbida en forma de radiación electromagnética.

Absorción
El espectro de absorción atómica de un elemento es único y corresponde a un conjunto de líneas negras correspondientes a las ondas electromagnéticas que han sido absorbidas por átomos de ese elemento, cuando se irradia la muestra con un haz de luz blanca.
Se hace incidir dicha luz sobre átomos en estado gaseoso contenidos en un tubo de vacío. La energía absorbida es empleada por el átomo para realizar transiciones electrónicas de los electrones desde el estado fundamental hacia estados excitados de mayor energía.



¿Cómo son los espectros de emisión del resto de elementos químicos de la tabla periódica?
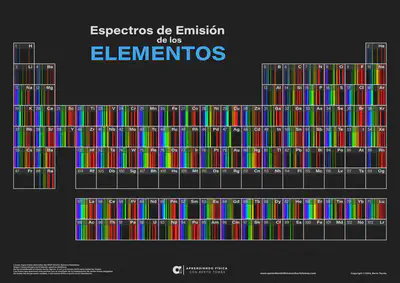
Si quieres aprender más sobre espectros atómicos te recomendamos leer esta interesante entrada del blog.
Postulados
Este modelo se basa en tres postulados fundamentales:
- Los electrones describen órbitas circulares en torno al núcleo sin irradiar energía.
- Solo están permitidas aquellas órbitas en las que el electrón tiene un momento angular múltiplo entero de $\hbar = h/(2\pi)$.
- El electrón solo emite o absorbe energía en los saltos de una órbita permitida a otra, siendo la energía emitida/absorbida la diferencia de energía entre ambos niveles.

Ecuación de Rydberg
La ecuación de Rydberg nos da la longitud de onda de las líneas espectrales de muchos elementos químicos.
Para el caso del hidrógeno:
$$ \frac{1}{\lambda} = R_\mathrm H\cdot\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right), $$donde $\lambda$ es la longitud de onda de la radiación emitida en el vacío, $R_\mathrm H = 1.097\times 10^7\thinspace \mathrm m^{-1}$ es la constante de Rydberg y $n_1$ y $n_2$ son los números cuánticos principales de las órbitas involucradas en el salto (con $n_2>n_1$).
Según cuál sea el nivel de energía al que vuelve el electrón excitado, tenemos diferentes series de bandas en el espectro:
Esta ecuación también nos permite calcular el valor energético correspondiente a una transición electrónica entre dos niveles dados, $\Delta E$:
$$ \Delta E = hcR_\mathrm H\cdot\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right), $$donde $h = 6.626\times 10^{-34}\thinspace\mathrm{J\thinspace s}$ es la constante de Planck y $c = 299\thinspace 792\thinspace 458\thinspace \mathrm{m/s}$ es la velocidad de la luz en el vacío.
Explora los modelos atómicos del hidrógeno y su relación con los espectros con esta magnífica simulación:
Orígenes de la teoría cuántica
(continúa hacia abajo)
👇
Radiación de cuerpo negro
Es la radiación electromagnética re-emitida por un cuerpo ideal que absorbe toda la radiación que incide sobre él (cuerpo negro), estando en equilibrio termodinámico con su entorno.

Tiene un espectro muy característico, inversamente relacionado con la intensidad, que depende únicamente de la temperatura del cuerpo.

El fallo de la teoría clásica vigente a la hora de explicar este espectro se conoce como la catástrofe ultravioleta.
Max Planck fue quien consiguió, en 1900, explicar el espectro del cuerpo negro, dando así origen a la teoría cuántica.
Aprende más sobre la radiación de cuerpo negro con esta excelente simulación:
¿Sabías que hemos creado lo más negro que hay en la Tierra? Manuel Alonso Orts nos lo cuenta en este 🧵 hilo:
¿Sabías que hemos creado lo más negro que hay en la Tierra? Está basado en nanotubos de carbono y cuando pinta máscaras, con él solo se ve oscuridad. Veamos en este hilo el origen, la evolución y la utilidad del Vantablack, el recubrimiento oscuro por excelencia. pic.twitter.com/lNqDa9llCu
— Manuel Alonso (@ManoloAlonso1) March 29, 2023
Hipótesis de Planck
En 1900, Planck propuso que la energía emitida, $E$, estaba relacionada con la frecuencia de oscilación de los átomos, $\nu$, según esta hipótesis:
La energía está cuantizada y solo puede ser emitida/absorbida en paquetes discretos llamados cuantos o fotones, múltiplos de la frecuencia $\nu$ de la radiación electromagnética asociada:
$$ E = h \nu = \frac{hc}{\lambda}, $$donde $h = 6.626\times 10^{-34}\thinspace\mathrm{J\thinspace s}$ es la constante de Planck.
Efecto fotoeléctrico
El efecto fotoeléctrico, observado por primera vez en 1887 por Hertz, consiste en la emisión de (foto)electrones cuando radiación electromagnética, como por ejemplo luz ultravioleta, incide sobre un material, típicamente metálico.
En 1905, Einstein aplica la hipótesis de Planck para explicar el fenómeno, recibiendo el Premio Nobel de Física en 1921 por ello. Explicó que la luz está constituida por fotones cuya energía viene dada por la relación de Planck-Einstein.
Características
- La cantidad de fotoelectrones emitidos es directamente proporcional a la intensidad de la radiación incidente.
- La emisión de fotoelectrones solo se produce cuando la radiación incidente tiene una frecuencia mayor o igual que una cierta frecuencia mínima, llamada frecuencia umbral o de corte, $\nu_0$, que es característica de cada material.
- La energía cinética de los fotoelectrones depende únicamente de la frecuencia de la radiación incidente.
- La emisión de fotoelectrones se realiza instantáneamente, sin existir ningún retraso entre la absorción de energía y la emisión de los fotoelectrones.

\begin{align*} E &= \phi + E_\mathrm c \\ h\nu &= h\nu_0 + E_\mathrm c \Rightarrow E_\mathrm c = h\left(\nu-\nu_0\right), \end{align*}
donde $h = 6.626\times 10^{-34}\thinspace\mathrm{J\thinspace s}$ es la constante de Planck, $\nu$ es la frecuencia de la radiación incidente, $\nu_0$ es la frecuencia umbral (cuya energía asociada, $\phi = h \nu_0$ se denomina función de trabajo o trabajo de extracción) y $E_\mathrm c = h\left(\nu-\nu_0\right)$ es la energía cinética máxima de los fotoelectrones, emitidos siempre que se cumpla $\nu \geq \nu_0$.
Si quieres aprender más sobre el efecto fotoeléctrico te recomendamos echar un vistazo a esta estupenda simulación.
Mecánica cuántica
(continúa hacia abajo)
👇
Dualidad onda-corpúsculo
Consiste en que el comportamiento de los objetos cuánticos no puede ser descrito considerando a estos como partículas u ondas, sino que tienen una naturaleza dual.

A partir de experimentos de difracción de electrones, Louis de Broglie fue el primero que propuso la siguiente hipótesis:
Toda partícula de masa $m$ moviéndose a una velocidad $v$ tiene asociada una onda cuya longitud de onda, $\lambda$, viene dada por
$$ \lambda = \frac{h}{mv}, $$siendo $h = 6.626\times 10^{-34}\thinspace\mathrm{J\thinspace s}$ la constante de Planck.
En el siguiente vídeo de Quantum Made Simple (en inglés) puedes aprender más sobre la dualidad onda-corpúsculo:
Principio de incertidumbre de Heisenberg
Existen ciertos pares de magnitudes físicas (aquellas cuyo producto tiene dimensiones de $\mathsf{M}\mathsf{L}^2\mathsf{T}^{-1}$), que no pueden ser determinadas simultáneamente con total exactitud, pues el producto de sus incertidumbres ha de ser mayor o igual que $h/(4\pi) = \hbar/2$.
Ejemplos de tales magnitudes son:
\begin{align*} \text{Posición $x$ y momento lineal $p$: } & \Delta x \cdot \Delta p \geq \frac{\hbar}{2} \\ \text{Energía $E$ y tiempo $t$: } & \Delta E \cdot \Delta t \geq \frac{\hbar}{2} \end{align*}
donde $\Delta$ denota la incertidumbre asociada y $\hbar = h/(2\pi)$.
El principio de incertidumbre de Heisenberg implica que, aunque se especifiquen todas las condiciones iniciales, no es posible predecir el valor de una cantidad con total certeza, dando así paso a una interpretación probabilística de la mecánica cuántica y el concepto de orbital atómico.
Orbitales atómicos
Son funciones matemáticas que describen el tamaño, la forma y la orientación de las regiones del espacio donde es posible encontrar al electrón.

Números cuánticos y su interpretación
En esta magnífica entrada, Adrián Castelo nos propone una forma de introducir los números cuánticos, estableciendo una analogía con el sonido.
Los números cuánticos describen valores de magnitudes físicas que se conservan en la dinámica de un sistema cuántico, tales como la energía o el momento angular, las cuales están cuantizadas y por tanto toman valores discretos.
Para describir completamente el estado cuántico de un electrón en un átomo necesitamos cuatro números cuánticos, los cuales tienen un significado orbital concreto.
Número cuántico principal $n$
Nos da el tamaño y la energía del orbital. Toma valores naturales ($1\leq n$), como por ejemplo $n = 1,2,3,\dots$
Número cuántico secundario $l$
Nos da la energía y forma del orbital. Puede tomar los siguientes valores:
$$ 0\leq l\leq n-1 $$de forma que, por ejemplo, para $n = 3$: $l=\\{0,1,2\\}$.
Número cuántico magnético $m_l$
Nos da la orientación del orbital. Puede tomar los siguientes valores:
$$ -l\leq m_l\leq l $$de forma que, por ejemplo, para $l = 2$: $m_l=\\{-2,-1,0,1,2\\}$.
Espín $m_s$
Es el momento angular intrínseco. Puede tomar los siguientes valores:
$$ -s\leq m_s\leq s $$Para un electrón, $s=1/2$, por lo que $m_s = \\{-1/2,1/2\\}$.
Conoce más sobre el espín en esta magnífica entrada del blog.
Estructura electrónica
(continúa hacia abajo)
👇
Principio de exclusión de Pauli
Dos o más electrones no pueden tener todos sus números cuánticos idénticos (ocupar el mismo estado cuántico) dentro del mismo sistema cuántico (átomo).
Gracias a este principio podemos determinar el número máximo de electrones que caben en cada tipo de orbital:
| Tipo de orbital | s | p | d | f |
|---|---|---|---|---|
| Número de orbitales | 1 | 3 | 5 | 7 |
| Número máximo de e– | 2 | 6 | 10 | 14 |
Orden energético creciente
La configuración electrónica es la distribución de los electrones de un átomo en orbitales atómicos (s, p, d y f).
Consulta aquí las reglas que se han de tener en cuenta a la hora de escribir la configuración electrónica de un átomo o un ion monoatómico.

Diagrama de Möller
El diagrama de Möller nos ayuda a saber en qué orden han de llenarse los distintos orbitales, siguiendo las flechas (orden energético creciente).

Los elementos que aparecen aquí en rojo son excepciones. Ejemplos notables son el Cu ([Ar] 4s1 3d10) y el Cr ([Ar] 4s1 3d5), debido a que los orbitales d son más estables cuando están llenos o semillenos, por razones de simetría.
Regla de Hund de la máxima multiplicidad
Al llenar orbitales de igual energía (por ejemplo los tres orbitales p) los electrones se distribuyen, siempre que sea posible, con sus espines paralelos, llenando los orbitales con la multiplicidad mayor.
Ejemplos
Se muestran también los números cuánticos del último electrón:

La configuración electrónica del nivel fundamental cumple que 1) minimiza la energía total de los electrones, (2) obedece el principio de exclusión de Pauli, (3) obedece la regla de Hund de la máxima multiplicidad y (4) considera la interacción de canje.
Partículas subatómicas
Tras los descubrimientos de Thomson, Rutherford y Chadwick a principios del siglo XX, parecía claro que el átomo estaba formado por protones y neutrones en su núcleo y una corteza donde estaban los electrones.
| Partícula | Masa/kg | Carga/C |
|---|---|---|
| Protón | $1.673\times 10^{-27}$ | $1.602\times 10^{-19}$ |
| Neutrón | $1.675\times 10^{-27}$ | $0$ |
| Electrón | $9.109\times 10^{-31}$ | $-1.602\times 10^{-19}$ |
Modelo estándar
Es la teoría que describe tres de las cuatro interacciones fundamentales de la naturaleza conocidas (electromagnética, nuclear fuerte y nuclear débil), además de clasificar todas las partículas elementales conocidas.

Descubre una interesante curiosidad sobre los muones en este magnífico hilo de BTeseracto:
Hablemos del muón, el hermano mayor del electrón. Cuando esta partícula se genera en la atmósfera, debería desaparecer mucho antes de llegar a la superficie del planeta. No obstante, llega. Y lo hace gracias a la relatividad especial. Imagen:Aspera European Astroparticle network. pic.twitter.com/XizxFvqnKG
— Bajo la sombra del teseracto (@BTeseracto) January 25, 2022
O aprende sobre cómo se pueden detectar los neutrinos y el misterio de los neutrinos solares desaparecidos en estos magníficos hilos también de BTeseracto:
Dicen que un neutrino puede atravesar más de un año luz de plomo sin enterarse siquiera que estaba ahí. Entonces, ¿cómo se puede detectar algo tan sigiloso? Para hacerlo tenemos que ser más inteligentes que el plomo. Hoy te contaremos cómo. pic.twitter.com/l5Ew4a4iPd
— Bajo la sombra del teseracto (@BTeseracto) February 3, 2022
Cada vez que en el Sol se fusionan dos protones, se genera un neutrino. Eso son muchos neutrinos. Neutrinos que no aparecían en nuestros detectores como esperábamos. Hoy toca astrofísica, física nuclear y el misterio de los neutrinos desaparecidos. Cred.: T2K-experiment. pic.twitter.com/DlehxLKsK4
— Bajo la sombra del teseracto (@BTeseracto) February 1, 2022
Evolución del Universo

Exportar a PDF
📥 Pincha aquí y sigue estas instrucciones:
- Abre el diálogo de Impresión (Control-P si estás en Windows).
- Cambia el Destino a Guardar como PDF.
- Cambia el Diseño a Horizontal.
- Cambia los Márgenes a Ninguno.
- Activa la opción Gráficos de fondo.
El proceso, en principio, solo funciona con Google Chrome.