Interacción gravitatoria
- Modelos cosmológicos
- Leyes de Kepler
- Ley de gravitación universal
- Momento angular
- Campo gravitatorio
- Movimiento de los satélites en órbitas
Descarga estas diapositivas en formato PDF 📥
Modelos cosmológicos
- Aristóteles (350 a. C.)
- Aristarco de Samos (300 a. C.)
- Ptolomeo (100 d. C.)
- Copérnico (s. XV)
- Galileo (s. XVI)
- Kepler (s. XVI–XVII)
(continúa hacia abajo)
👇
Aristóteles (350 a. C.)
Era un modelo geocéntrico, con la Tierra en el centro del Universo, rodeada por esferas transparentes de distintos tamaños en las que se encontraban los diferentes planetas.
La esfera más externa era en la que se encontraban las estrellas fijas. Dicha esfera giraba a un ritmo constante en torno a un eje que pasaba por la estrella polar.
Su movimiento era transmitido a las esferas de planetas más externos por rozamiento y así sucesivamente. Era, por tanto, un universo mecánico.
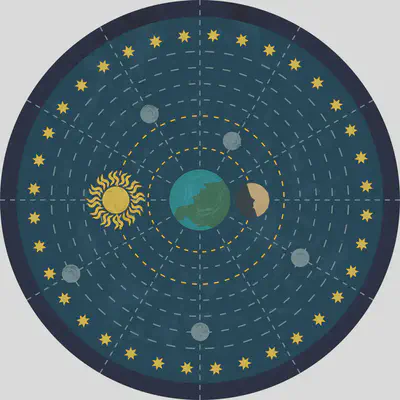
Como el mundo celeste era perfecto, los objetos en él solo podían describir órbitas circulares puesto que el círculo era el símbolo de la perfección.
Este modelo podía explicar muchas de las observaciones, pero no explicaba, por ejemplo:
- Variaciones observadas en el brillo del Sol (debidas a cambios en la distancia a la Tierra).
- Movimientos retrógrados observados en algunos planetas que, aparentemente, cambian el sentido de su movimiento.
Aristarco de Samos (300 a. C.)
No se suele mencionar pero fue el primer modelo heliocéntrico. En su modelo, el Sol se situaba en el centro del Universo y el resto de los planetas giraban en torno a él en órbitas circulares de distintas dimensiones.
El modelo de Aristarco también suponía que la Tierra describía un movimiento de rotación alrededor de su eje que permitía explicar fácilmente el día y la noche.
A pesar de que este modelo era bastante acertado, no prosperó por razones de índole filosófica:
- Paralaje de las estrellas fijas: deberían verse en diferente posición dependiendo de la época del año. Aristarco lo justificó de forma esencialmente correcta: dado que la distancia a las estrellas es mucho mayor que el diámetro de la órbita terrestre, no se aprecia paralaje.
- Implicaciones mecánicas del movimiento de rotación terrestre. Si arrojamos una piedra desde una torre, no debería caer en su base, sino a cierta distancia, pero las observaciones no se correspondían. Esto era una afirmación claramente errónea, pero para comprenderlo se necesitaba conocer el principio de inercia de Galileo (lo que más tarde sería la 1ª ley de Newton), desconocido para los griegos.
Ptolomeo (100 d. C.)
Propuso un modelo también geocéntrico introduciendo ciertas variaciones al modelo de Aristóteles, como que los planetas podían describir movimientos circulares o una composición de estos.
Para ello, introdujo varios artificios matemáticos, como los epiciclos, el deferente y el ecuante. Encajando todos estos artificios, Ptolomeo consiguió un sistema útil para astrónomos y navegantes, que perduró más de 14 siglos.
Copérnico (s. XV)
Propuso un modelo heliocéntrico igual que el de Aristarco (Sol en el centro con planetas orbitando alrededor y rotación de la Tierra).
Este modelo explicaba de forma mucho más sencilla los movimientos retrógrados, que eran causados por la combinación entre el movimiento terrestre y el de los planetas.
Presentaba varias ventajas sobre el geocéntrico:
- Simplicidad: se requieren muchos menos movimientos para explicar las observaciones.
- Modelo único: todos los planetas se ajustan de igual forma al modelo.
Sin embargo, tardó más de un siglo en ser aceptado por el rechazo a perder la cosmología aristotélica, los dogmas y porque no existía ninguna observación que un modelo geocéntrico no pudiera explicar.
Galileo (s. XVI)
Aprende más sobre Galileo Galilei echando un vistazo a su biografía científica en nuestra sección de Historia de la Ciencia.
Perfeccionó el telescopio y esto permitió mejorar enormemente las observaciones. Así, descubrió las fases de Venus, que únicamente podían ser explicadas de forma satisfactoria considerando un modelo heliocéntrico (se consideró la prueba empírica definitiva).
Kepler (s. XVI–XVII)
Estableció las tres leyes que llevan su nombre, con las que fue de capaz de explicar a la perfección las observaciones.
Leyes de Kepler
(continúa hacia abajo)
👇
Constituyen una descripción cinemática del Sistema Solar y consiguen explicar de forma muy precisa todas las observaciones relativas no solo al movimiento de planetas, sino también asteroides, cometas y satélites (incluso artificales).
1ª ley: órbitas elípticas
Los planetas giran en torno al Sol describiendo órbitas elípticas, con el Sol situado en uno de los focos.
2ª ley: ley de las áreas
$$ \frac{\mathrm d A}{\mathrm d t} = \text{constante} $$Los planetas se mueven con velocidad areolar constante, es decir, el radio vector barre áreas iguales en tiempos iguales.
3ª ley: ley de los periodos
$$ \frac{T^2}{r^3} = \text{constante} $$El cuadrado del periodo orbital de los planetas es directamente proporcional al cubo de su distancia media al Sol.
donde $r\rightarrow a$ (semieje mayor) si la órbita es elíptica.
Explora las leyes de Kepler con esta magnífica simulación:
Ley de gravitación universal de Newton
Teniendo en cuenta las leyes de Kepler, Newton llegó a la conclusión de que el movimiento de los planetas era debido a una fuerza de atracción proporcional a la masa del planeta ($m$) y del Sol ($M$) e inversamente proporcional al cuadrado de la distancia que los separa ($r$):
donde $\hat{\mathrm r}$ es el vector unitario que va de $M$ a $m$ y $G = 6.67\times 10^{11}\,\mathrm N \,\mathrm m^2\,\mathrm{kg}^{-2}$ es la constante de gravitación universal, determinada experimentalmente por Henry Cavendish en 1798 utilizando una balanza de torsión.
Medida experimental de $G$
La constante de gravitación universal, $G$, fue determinada experimentalmente 100 años después de Newton por el científico británico y francés Henry Cavendish.
Para ello, empleó una balanza de torsión:
Experimenta con este laboratorio de fuerza de gravedad:
Esta ley no solo es aplicable a cuerpos celestes, sino que también se cumple para dos masas cualesquiera (caída de cuerpos). Se conoce como ley de gravitación universal y es revolucionaria por muchas razones:
- Ruptura de la barrera cielo-Tierra.
- Acción a distancia.
También es aplicable a un conjunto de masas puntuales, pues cumple el principio de superposición:
$$ \vec F_\mathrm t = \sum_i \vec F_i $$Relación con la 3ª ley de Kepler
En el movimiento de un planeta alrededor del Sol, la fuerza gravitatoria actúa como fuerza centrípeta.
Suponiendo una órbita circular, podemos relacionar la velocidad orbital con el periodo, $v = 2\pi r/T$:
$$ \begin{aligned} F_\mathrm g & = F_\mathrm c \\ \frac{GM\cancel m}{r^2} & = \frac{\cancel mv^2}{r} \\ \frac{GM}{r^2} & = \frac{4\pi^2 r^{\cancel 2}}{T^2 \cancel r} \\ \frac{T^2}{r^3} & = \frac{4\pi^2}{GM} \end{aligned} $$Esto nos permite determinar la masa de un planeta conociendo el periodo y el radio orbital de uno de sus satélites:
$$ M = \frac{4\pi^2r^3}{GT^2} $$
Momento angular
Newton demostró que la fuerza gravitatoria es una fuerza central, ya que está dirigida hacia un centro fijo (como el Sol) y depende únicamente de la distancia al mismo.
Cuando las fuerzas son centrales, existe una magnitud, llamada momento angular, que se conserva, lo que facilita enormemente la descripción de muchos fenómenos asociados.
Recordando que el momento lineal $\vec p = m\vec v$ representa la inercia en un movimiento de traslación, se define el momento angular como la magnitud análoga para la rotación:
$$ \vec L = \vec r\times \vec p = \vec r\times m\vec v $$
Conservación del momento angular
Una magnitud se conserva cuando permanece constante, es decir, no cambia con el tiempo. Estudiemos la variación de $\vec L$ con el tiempo para ver en qué circunstancias se conserva:
$\vec L$ se conserva si su variación con el tiempo es cero:
Movimientos planetarios
La conservación de $\vec L$ implica:
-
Dirección de $\vec L$ no cambia $\Rightarrow$ órbitas planas (plano $\perp$ a $\vec L$).
-
Sentido de $\vec L$ no cambia $\Rightarrow$ planetas siempre giran en el mismo sentido.
-
Módulo de $\vec L$ es constante:
$$ \begin{aligned} L_1 &= L_2 \\ r_1 \cancel mv_1\sin\theta_1 &= r_2 \cancel mv_2\sin\theta_2 \end{aligned} $$
En órbitas circulares: $r_1 = r_2; \theta_1 = \theta_2 = 90°\Rightarrow v_1 = v_2$ ($v$ constante).
En órbitas elípticas: $r_\mathrm pv_\mathrm p = r_\mathrm av_\mathrm a$ (p $\rightarrow$ periastro, a $\rightarrow$ apoastro).
2ª ley de Kepler
La conservación de $\vec L$ también explica la 2ª ley de Kepler.
El área barrida en $\mathrm d t$ se puede aproximar por el área de un triángulo isósceles:
Campo gravitatorio
- Campo gravitatorio creado por una masa puntual
- Relación fuerza-campo
- Potencial gravitatorio
- Energía potencial gravitatoria
- Trabajo realizado por la fuerza gravitatoria
- Representación del campo gravitatorio
- Campo gravitatorio creado por distribuciones esféricas de masa
- Campo gravitatorio terrestre
(continúa hacia abajo)
👇
La ley de gravitación universal introdujo la idea de acción a distancia. ¿Cómo puede un objeto influenciar a otro sin estar en contacto con él? Hubo varios intentos de explicar cómo se producía la interacción a distancia.
Algunos científicos afirmaban que existía una sustancia llamada éter que llenaba el vacío (fluido) y era la responsable de transmitir la interacción.
Este éter no se sabía de qué estaba hecho y su existencia no podía demostrarse experimentalmente, pero se mantuvo durante algún tiempo.
Científicos posteriores demostraron que la interacción a distancia se producía también en el vacío, por lo que la existencia del éter no era necesaria.
Finalmente, Einstein justificó la acción a distancia por una perturbación en el espacio-tiempo debida a la presencia de una masa. Dicha perturbación se denominó campo gravitatorio.
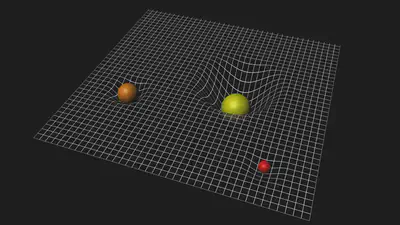
Campo gravitatorio creado por una masa puntual
El campo gravitatorio $\vec g$ creado por una masa puntual $M$ en un punto cualquiera que se encuentra a una distancia $r$ de ella viene dado por:
$$ \vec g = -\frac{GM}{r^2}\,\hat{\mathrm r} $$y se mide en N/kg o m/s2 en el SI.
Distribución de masas puntuales
Cuando en una misma región del espacio existen varias ($n$) masas puntuales, el campo gravitatorio total es la suma vectorial de los campos creados por cada una de las masas, resultado que se conoce como principio de superposición:
\[ \vec g_\mathrm t = \sum_{i=1}^n \vec g_i = \sum_{i=1}^n \left(-\frac{GM_i}{r_i^2}\,\hat{\mathrm r}_i\right) \]Relación fuerza-campo
La fuerza $\vec F_\mathrm g$ que actúa sobre una masa $m$ colocada en un punto del espacio en el que existe un campo gravitatorio $\vec g$ viene dada por:
\[ \vec F_\mathrm g = m\vec g, \]expresión que coincide con la ley de gravitación universal de Newton:
\[ \vec F_\mathrm g = m\vec g = -m\frac{GM}{r^2}\,\hat{\mathrm r} = -\frac{GMm}{r^2}\,\hat{\mathrm r} \]Potencial gravitatorio
Como la fuerza gravitatoria es conservativa, el campo gravitatorio $\vec g$ puede expresarse en función de un potencial gravitatorio $V$.
Este se define como el trabajo por unidad de masa que debe realizar una fuerza para traer un cuerpo desde el infinito (donde $V=0$ por convenio) hasta un punto P, a velocidad constante:
tal que $\vec g = -\dfrac{\mathrm d V}{\mathrm d r}\,\hat{\mathrm r}$ (en general $\vec g = -\nabla V$, siendo $\nabla$ el operador diferencial vectorial nabla).
Distribución de masas puntuales
El potencial generado por una distribución de masas puntuales en un punto es la suma de los potenciales generados por cada una de las masas en dicho punto:
\[ V_\mathrm t = \sum_{i=1}^n V_i = \sum_{i=1}^n \left(-\frac{GM_i}{r_i}\right) \]Energía potencial gravitatoria
La energía potencial gravitatoria, $E_\mathrm p$, es la energía que adquiere una masa $m$ dentro de un campo gravitatorio $\vec g$.
Se define como el trabajo que debe realizar una fuerza para traer un cuerpo desde el infinito (donde $E_\mathrm p=0$ por convenio) hasta un punto P, a velocidad constante:
También se puede calcular a partir del potencial gravitatorio:
\[ E_\mathrm p = mV = -\frac{GMm}{r} \]El signo $-$ indica que la masa está ligada al campo gravitatorio (si $E_\mathrm p > 0$ estaría fuera del campo).
Trabajo realizado por la fuerza gravitatoria
Cuando una masa $m$ se mueve libremente dentro de un campo gravitatorio, se realiza un trabajo $W_{1\rightarrow 2}$ tal que:
que solo depende de las posiciones inicial y final, lo que significa que $\vec F_\mathrm g$ es conservativa.
Representación del campo gravitatorio
Existen dos maneras de representar el campo gravitatorio:
(continúa hacia abajo)
👇
Líneas de campo
Son tangentes al campo gravitatorio en cada punto. Cumplen que:
- Nunca se cortan (supondría que en un mismo punto habría dos valores de campo, lo que es imposible).
- El número de líneas es proporcional a la intensidad del campo gravitatorio.
Superficies equipotenciales
Son regiones en las que el potencial gravitatorio tiene el mismo valor. Cumplen que:
- Nunca se cortan.
- Siempre son perpendiculares a las líneas de campo.
Campo gravitatorio creado por distribuciones esféricas de masa
Hasta ahora hemos visto el campo creado por masas puntuales, sin extensión. Podemos aproximar que una masa es puntual cuando sus dimensiones son mucho menores que la distancia considerada. Es decir, cuando trabajamos en regiones del campo que están alejadas de la masa que lo genera; por ejemplo, en el Sistema Solar.
Cuando las dimensiones no son despreciables frente a la distancia, hay que considerar el tamaño y la geometría del objeto. Esto sucede, por ejemplo, cuando consideramos el campo en la superficie de terrestre o en sus proximidades.
En ese caso, para el cálculo de $\vec g$ se requiere emplear un teorema matemático: el teorema de Gauss.
Antes de enunciar el teorema hay que definir el flujo $\symup\Phi = \oint_S \vec g \cdot \mathrm d \vec s$, como el número de líneas de campo que atraviesa una superficie.
El teorema de Gauss nos permite relacionar el flujo neto $\Phi$ que atraviesa una superficie cerrada $S$ con la masa encerrada $M_\mathrm{encerrada}$ por dicha superficie:
\[ \Phi = -4\pi GM_\mathrm{encerrada} \]Campo creado por una esfera hueca
Una esfera que solo tiene masa en su superficie:
Campo creado por una esfera maciza homogénea
Una esfera con densidad homogénea $\rho$:
- Para $r \leq R$:
- Para $r \geq R$:
Campo gravitatorio terrestre
Lo que acabamos de ver para una esfera maciza homogénea también es aplicable a esferas con capas homogéneas concéntricas, por lo que podemos aplicarlo a la Tierra:
$$ \vec g = -\frac{GM_\mathrm T}{r^2}\,\hat{\mathrm r} \quad \mathrm{para}\ r=R_\mathrm T+h\geq R_\mathrm T\ (h\geq 0) $$La realidad es un poco más complicada. A día de hoy tenemos el llamado Modelo de Referencia Preliminar (PREM por sus siglás en inglés):
En esta práctica virtual diseñada para 1.º de Bachillerato, el Departamento de Física y Química del IES Valle del Saja nos propone dos métodos bien diferentes pero igual de eficaces para determinar el valor de la aceleración de la gravedad terrestre:
Aquí puedes descargarte el guion de la práctica.
Variación de $\vec g$ con la altura
En la superficie terrestre $r = R_\mathrm T$ y por lo tanto:
$$ g_0 = \frac{GM_\mathrm T}{R_\mathrm T^2} $$A una altura $h$ sobre la superficie:
Variación de $\vec g$ con la latitud
Al igual que con la altura, la gravedad varía con la latitud. Consideremos un punto P tal como indica la figura:
El punto P gira debido a la rotación de la Tierra, describiendo una circunferencia de radio $r$.
Al ser un sistema de referencia no inercial, aparece una aceleración centrífuga (ficticia), la cual resulta conveniente descomponer en ejes radial y tangencial:
$$ \vec a_\mathrm{cf} = a_{\mathrm{cf}_\mathrm r}\,\hat{\mathrm r} + a_{\mathrm{cf}_\mathrm t}\,\hat{\mathrm t}, $$donde $a_{\mathrm{cf}_\mathrm r} = a_\mathrm{cf}\cos\varphi = \omega^2 r \cos\varphi = \omega^2R_\mathrm T\cos^2\varphi$.
El punto P siente una gravedad efectiva inferior ya que la componente radial algo contrarresta:
¿Cómo se clasifican las órbitas de los satélites que giran en torno a la Tierra?
(continúa hacia abajo)
👇
En función de la latitud
- Órbitas polares ($\varphi = 90°$).
- Órbitas ecuatoriales ($\varphi = 0°$).
- Órbitas inclinadas.
En función de su forma
- Circulares.
- Elípticas (cobertura a mayor altitud).
- No geocéntricas (exploraciones interplanetarias).
En función de la altura sobre la superficie
</figcaption>
Movimiento de los satélites en órbitas
(continúa hacia abajo)
👇
Supongamos que un satélite describe una órbita circular a una altura $h$ ($r=R+h$) sobre la superficie de un planeta, con MCU. Si el satélite permanece en la órbita, debe cumplirse:
$$ \begin{aligned} F_\mathrm g & = F_\mathrm c \\ \frac{GM\cancel m}{r^{\cancel 2}} & = \frac{\cancel mv^2}{\cancel r} \end{aligned} $$de donde podemos obtener:
- Velocidad orbital: $\displaystyle v = \sqrt{\frac{GM}{R+h}}$
- Periodo de revolución: $\displaystyle T = 2\pi\sqrt{\frac{\left(R+h\right)^3}{GM}}$
- Frecuencia: $f=1/T$
Satélites geoestacionarios
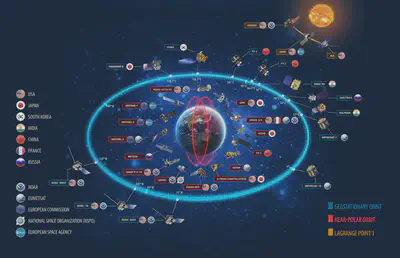
Son aquellos cuyo periodo coincide con el periodo de rotación terrestre, de forma que orbitan manteniéndose siempre en la misma vertical (aparentemente no se mueven). Se colocan en el plano del ecuador para que $\vec g$ no varíe con la latitud.
Despejando de la 3ª ley de Kepler:
Energía de los satélites
Cuando describe una órbita, la energía mecánica de un satélite viene dada por:
Si tenemos en cuenta que todas las fuerzas que actúan son conservativas, la energía mecánica se conserva.
Así, es posible calcular:
- Velocidad de lanzamiento
- Es la velocidad que hay que comunicar a un satélite para colocarlo en su órbita, suponiendo que se lanza desde la superficie terrestre:
- Velocidad de escape
- Si en el lanzamiento proporcionamos al satélite una velocidad suficientemente elevada, este puede llegar a escapar del campo gravitatorio terrestre. A esta (mínima) velocidad se le denomina velocidad de escape.
Imponiendo la condición de que el objeto se aleje hasta una distancia infinita y quede en reposo ($E=0$):
$$ \begin{aligned} E & = 0 \\ \frac{1}{2}mv_\mathrm e^2 - \frac{GM_\mathrm T m}{R_\mathrm T} & = 0 \rightarrow v_\mathrm e = \sqrt{\frac{2GM_\mathrm T}{R_\mathrm T}} \end{aligned} $$Para $v\geq v_\mathrm e$ el satélite escapa de la influencia de $\vec g$ y se mueve libremente. Es importante destacar, a la vista de la expresión, que solo depende de $M_\mathrm T$ y de $R_\mathrm T$ (es independiente de las características del satélite).
- Trabajo para pasar de una órbita a otra
- Supongamos que queremos pasar un satélite de una órbita 1 a otra órbita 2. Será necesario realizar un trabajo tal que:
Energía de los satélites y tipo de órbita
La energía de un satélite determina el tipo de órbita que describe:
\[ E = \overbrace{\frac{1}{2}mv^2}^{+}\overbrace{-\frac{GMm}{r}}^{-} \]$E<0$ Ligado al campo (órbitas cerradas):
$E\geq 0$ No ligado al campo (órbitas abiertas):
Exportar a PDF
📥 Pincha aquí y sigue estas instrucciones:
- Abre el diálogo de Impresión (Control-P si estás en Windows).
- Cambia el Destino a Guardar como PDF.
- Cambia el Diseño a Horizontal.
- Cambia los Márgenes a Ninguno.
- Activa la opción Gráficos de fondo.
El proceso, en principio, solo funciona con Google Chrome.