Inducción electromagnética
- Experiencias de Faraday y de Henry
- Flujo eléctrico y fem inducida
- Ley de Faraday-Henry y ley de Lenz
- Autoinducción e inducción mutua
- Generación de corrientes alternas y aplicaciones
- Electromagnetismo
Descarga estas diapositivas en formato PDF 📥
Introducción
En el anterior tema vimos que el primer científico que relacionó la electricidad y el magnetismo fue Ørsted (1777–1851).
En sus experimentos, demostró que una corriente eléctrica era capaz de generar un campo magnético.
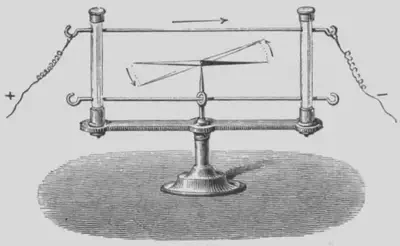
Poco después, el físico Michael Faraday (1791–1867) llevó a cabo una serie de experiencias que le permitieron afirmar que la variación de un campo magnético puede inducir una corriente eléctrica (el proceso opuesto a Ørsted).
Simultáneamente, otro científico estadounidense llamado Joseph Henry (1797–1878) llegó a la misma conclusión, aunque publicó sus resultados algo más tarde que Faraday.
En este tema estudiaremos este fenómeno conocido como inducción electromagnética: producción de una corriente eléctrica por la acción de un flujo magnético variable en el tiempo.
Experiencias de Faraday y de Henry
(continúa hacia abajo)
👇
Experiencias de Faraday
(continúa hacia abajo)
👇
1ª experiencia
Se dispone de una espira conectada a un galvanómetro (dispositivo que mide, en este caso, el paso de corriente eléctrica I).
Se observa que si se aleja o se acerca un imán a la espira se produce en ella una corriente inducida, cuyo sentido depende del polo del imán que se emplee y si este se acerca o se aleja de la espira.
2ª experiencia
Emplea un montaje similar sustituyendo la espira por un solenoide. Se observa lo mismo pero de forma más acusada (resulta más fácil medir la I inducida en el solenoide).
3ª experiencia
Se dispone de un solenoide conectado a una fuente con un interruptor. Paralelo a él hay otro solenoide conectado a un galvanómetro.
Experiencia de Henry
Henry descubrió que, cuando un conductor se movía perpendicularmente a un campo magnético, entre sus extremos aparecía una diferencia de potencial. Si el conductor forma parte de un circuito, en él aparece una corriente inducida.
Existen otras muchas experiencias de inducción electromagnética.
Por ejemplo, para generar corrientes alternas (aquellas cuyo sentido de circulación es variable), se utiliza:
Flujo magnético y fem inducida
(continúa hacia abajo)
👇
Flujo magnético
Para poder explicar los fenómenos de inducción electromagnética, resulta imprescindible definir previamente el flujo magnético, $\symup\Phi$, que atraviesa una superficie $S$ de un circuito cerrado, relacionado con el número de líneas de campo que atraviesa la superficie.
Viene dado por:
$$ \symup\Phi = \int_S \vec B\cdot \mathrm d \vec S = \int_S B\mathrm d S\cos\theta, $$donde $\mathrm d \vec S$ es el vector superficie cuya dirección es perpendicular a la superficie y cuyo sentido es hacia afuera, $\vec B$ es el campo magnético, $\theta$ es el ángulo entre $\vec B$ y $\mathrm d \vec S$. Su unidad en el SI es el weber (Wb ≡ V s).
Inducción electromagnética
La inducción se debe a una variación de flujo magnético, la cual puede producirse por tres causas diferentes:
- Cambia $\vec B$ con el tiempo: experiencias de Faraday.
- Cambia $\theta$ con el tiempo: experiencia de la corriente alterna.
- Cambia $S$ con el tiempo: experiencia de Henry.
Además, de las anteriores experiencias se deduce el sentido de la corriente inducida, ya que esta será tal que genere un campo magnético inducido que se opone a la variación del flujo que la produce:
- Si $\symup\Phi$ aumenta con el tiempo: $I_\mathrm{ind}$ da lugar a $\vec B_\mathrm{ind}$ que tiende a disminuir $\symup\Phi$.
- Si $\symup\Phi$ disminuye con el tiempo: $I_\mathrm{ind}$ da lugar a $\vec B_\mathrm{ind}$ que tiende a aumentar $\symup\Phi$.
Fuerza electromotriz (fem) inducida
Para comprender bien por qué al variar el flujo magnético se produce una corriente inducida, consideraremos la experiencia de Henry:
Supongamos que el conductor tiene una longitud $\ell$ y se mueve con velocidad $\vec v$ en una región en la que existe un $\vec B$ uniforme ($\vec v\perp\vec B$).
Los electrones del conductor, debido a $\vec B$, se verán sometidos a una fuerza magnética $\vec F_\mathrm m$ dada por la ley de Lorentz:
$$ \vec F_\mathrm m = q\vec v\times \vec B $$A medida que avanza el proceso, prácticamente instantáneo, se produce una separación de cargas (cationes y electrones) y aparece, por tanto, una diferencia de potencial $\symup\Delta V$ y un campo eléctrico $\vec E$.
Así, los electrones también se verán sometidos a una fuerza eléctrica $\vec F_\mathrm e$ tal que:
\[ \vec F_\mathrm e = q\vec E \]Se alcanza el equilibrio en el que $F_\mathrm e = F_\mathrm m \Rightarrow E=vB$. El campo eléctrico permanece constante siempre que el conductor se mueva con velocidad constante.
Si conectamos el conductor a un circuito:
Para que la $I_\mathrm{ind}$ se mantenga es necesario mantener la $\symup\Delta V$ o equivalentemente la separación entre cargas. En nuestro caso la responsable es la velocidad del conductor, que hace que $\vec F_\mathrm m \neq \vec 0$ y los electrones comiencen a moverse. Para que se mueva el conductor debemos aplicar un $W_\mathrm{ext}$.
Así, podemos definir la fuerza electromotriz fem ($\mathcal{E}$) como el trabajo realizado por unidad de carga para mantener la diferencia de potencial:
\[ \mathcal{E} = \frac{W_\mathrm{ext}}{q}\quad\text{Unidad en el SI: V (voltio)} \]Normalmente, es proporcionada por un generador eléctrico.
Ley de Faraday-Henry y ley de Lenz
En las diferentes experiencias hemos visto que aparece una corriente inducida cuando el flujo magnético varía con el tiempo, y que se debe a la fem. Además, depende también de la resistencia del conductor.
Para calcular y relacionar estas magnitudes se tienen en cuenta las siguientes leyes:
(continúa hacia abajo)
👇
Ley de Faraday-Henry
El valor de la fem inducida en un circuito es igual a la variación temporal del flujo magnético que lo atraviesa:
\[ \mathcal{E} = \frac{\mathrm d\symup\Phi}{\mathrm d t} \]
Ley de Lenz
El sentido de la corriente inducida es tal que se opone al efecto que la produce:
\[ \mathcal{E} = -\frac{\mathrm d\symup\Phi}{\mathrm d t} \]
Si $\symup\Phi$ aumenta con $t$, la $I_\mathrm{ind}$ genera un $\vec B_\mathrm{ind}$ opuesto al $\vec B_\mathrm{inicial}$.
Si $\symup\Phi$ disminuye con $t$, la $I_\mathrm{ind}$ genera un $\vec B_\mathrm{ind}$ igual al $\vec B_\mathrm{inicial}$.
Ejemplos
Una vez hemos calculado la fem inducida, podemos calcular la ley de Ohm:
\[ I_\mathrm{ind} = \frac{\mathcal{E}}{R} = -\frac{1}{R}\frac{\mathrm d\symup\Phi}{\mathrm d t}, \]donde $R$ se mide en ohmios ($\symup\Omega$) e $I_\mathrm{ind}$ se mide en amperios (A) en el SI.
Autoinducción e inducción mutua
(continúa hacia abajo)
👇
Autoinducción
La autoinducción consiste en la inducción de una corriente sobre sí misma. Para que se produzca, es necesario que la corriente que recorre un circuito varíe con el tiempo.
Consideremos un solenoide de longitud $\ell$ y radio $R$ formado por $N$ espiras. El solenoide forma parte de un circuito en el que existe un generador de corriente continua y cuya resistencia es $r$.
El campo generado por el solenoide, $\vec B$, es paralelo a su eje y en su interior toma un valor constante:
\[ B = \frac{\mu NI}{\ell} \]Por lo tanto, el flujo que atraviesa el solenoide:
\[ \symup\Phi = BS\cos\theta = BS = \frac{\mu NI}{\ell}\cdot N\pi R^2 = \frac{\mu N^2\pi R^2}{\ell}I = LI, \]donde $L = \mu N^2 \pi R^2/\ell$ es el coeficiente de autoinducción, constante definida por las características del solenoide, cuyas unidades en el SI son los henrios (H).
Solo aparecerá corriente inducida si $I$ es variable (p. ej. corriente alterna). En ese caso aparecerá en el solenoide otra intensidad, $I_\mathrm{autoind}$, que se opone a la variación del flujo.
La fem autoinducida correspondiente, $\mathcal{E}'$, vendrá dada por:
\[ \mathcal{E}' = -\frac{\mathrm d\symup\Phi}{\mathrm d t} = -L\frac{\mathrm d I}{\mathrm d t} \]Así, la fem autoinducida depende de la rapidez con la que varía $I$ y se opone a la variación:
\[ I_\mathrm{autoind} = \frac{\mathcal{E'}}{r} = -\frac{L}{r}\frac{\mathrm d I}{\mathrm d t}\quad\text{(ley de Ohm)} \]Inducción mutua
Hasta ahora hemos visto que un circuito inductor genera una corriente inducida en otro circuito, el inducido. Pero no hemos considerado el efecto que este segundo circuito (inducido) tiene en el primero (inductor). A este fenómeno se le denomina inducción mutua.
Consideremos dos solenoides:
- Solenoide 1
- $N_1$ espiras, longitud $\ell_1$, unido a un circuito por el que circula $I_1$ y tiene una resistencia $r_1$.
- Solenoide 2
- $N_2$ espiras, longitud $\ell_2$, unido a un circuito en el que hay un galvanómetro que permite medir el paso de la corriente $I_2$.
Cuando aparece $I_1$ en el solenoide 1 se genera $B_1$ tal que:
\[ B_1 = \frac{\mu N_1 I_1}{\ell} \]Este campo atraviesa las espiras del solenoide 2, generando un flujo magnético $\symup\Phi_2$ tal que:
\[ \symup\Phi_2 = B_1 N_2 S = \frac{\mu N_1 N_2 S}{\ell} I_1 = M_{12}I_1, \]donde $M_{12} = \mu N_1 N_2 S/\ell$ es el coeficiente de inducción mutua que ejerce 1 sobre 2.
Si $I_1$ varía con el tiempo, $\symup\Phi_2$ es variable y aparece una corriente inducida y fem:
\[ \mathcal{E}_2 = -M_{12}\frac{\mathrm d I_1}{\mathrm d t} \]El fenómeno también se produce a la inversa:
\[ \mathcal{E}_1 = -M_{21}\frac{\mathrm d I_2}{\mathrm d t} \]Es fácil demostrar que $M_{12} = M_{21} = M = \mu N_1 N_2 S/\ell$.
Generación de corrientes alternas y aplicaciones
(continúa hacia abajo)
👇
Generación de corrientes alternas
Se entiende por corriente alterna aquella cuyo sentido de circulación es variable, dinstinguiéndose así de la corriente continua.
La generación de corrientes alternas se basa en la inducción electromagnética, específicamente en la variación de un flujo magnético.
Suponiendo una espira que gira con velocidad angular $\omega$, el flujo magnético que la atraviesa viene dado por:
\[ \symup\Phi = BS\cos\theta = BS\cos \omega t, \]por lo que la fem inducida viene dada por la ley de Faraday-Henry:
\[ \mathcal{E} = -\frac{\mathrm d\symup\Phi}{\mathrm d t} = BS\omega\sin\omega t \]En el caso de una bobina de $N$ espiras, la fem puede expresarse como:
\[ \mathcal{E} = \mathcal{E}_0\sin\omega t\quad\text{con }\mathcal{E}_0=NBS\omega \]Si consideramos que el generador descrito está integrado en un circuito sencillo que consta solamente de una resistencia $r$, aplicando la ley de Ohm puede obtenerse la intensidad inducida, que varía sinusoidalmente:
\[ I = \frac{\mathcal{E}}{r} = I_0\sin\omega t\quad\text{con }I_0=\frac{\mathcal{E}_0}{r} \]Aplicaciones de la inducción electromagnética
(continúa hacia abajo)
👇
Generadores de corriente alterna (alternadores)
Un generador eléctrico es un dispositivo que transforma la energía mecánica en energía eléctrica.
Los generadores más sencillos están constituidos por un bobinado que gira en el seno de un campo magnético uniforme, aunque esta configuración no es útil cuando se requieren potencias elevadas.
Es por eso que los alternadores actuales se construyen de forma que la parte que gira es el electroimán (rotor) y la parte que permanece fija es el bobinado (estator).
Motores
Los motores de corriente alterna transforman energía eléctrica en energía mecánica, justo al contrario de lo que sucede en los alternadores.
En la siguiente figura se esquematiza su funcionamiento:
Transformadores
La importancia de las corrientes alternas reside en la eficiencia con la que permiten transportar la energía eléctrica.
Entre un generador eléctrico y el punto de consumo de la energía eléctrica se producen, de forma ineludible, pérdidas debidas al efecto Joule, que tienen lugar en las líneas de transporte.
Para reducir estas pérdidas deben emplearse materiales con la mínima resistencia posible. Además, cuanto menor sea la intensidad de corriente, o equivalentemente mayor sea el voltaje, menores serán las pérdidas.
Esto último hace que la corriente alterna pueda transportarse de forma mucho más eficiente que la continua, puesto que puede incrementarse el voltaje en la salida del generador, transportarse por las líneas de alta tensión y reducirlo de nuevo a su valor de consumo (220 V en España) antes de llegar al punto de consumo.
Esto se consigue con la ayuda de transformadores, dispositivos capaces de transmitir la energía eléctrica de un circuito de corriente alterna a otro, sin modificar su frecuencia.
Esta transmisión va acompañada de un cambio de voltaje de forma que cuando el transformador devuelve una tensión más alta, se denomina elevador, y cuando devuelve una tensión más baja, se dice que es un reductor.
Así, la energía eléctrica se transfiere del primario al secundario, cumpliéndose:
\[ \frac{\mathcal{E}_1}{\mathcal{E}_2} = \frac{N_1}{N_2} = \frac{I_2}{I_1} \]Aprende más sobre inducción electromagnética con esta excelente simulación:
Electromagnetismo
Esta sección, dedicada al estudio de campos eléctricos y magnéticos dependientes del tiempo, queda fuera de los saberes básicos de Física de 2.º Bach y la incluímos aquí solo por completitud.
El estudio del electromagnetismo usualmente comienza analizando por separado el campo eléctrico, cuya fuente son las cargas eléctricas, y el campo magnético, generado por corrientes eléctricas.
Sin embargo, ambos campos están íntimamente relacionados, tal y como acabamos de ver en los fenómenos de inducción electromagnética.
En este apartado veremos cómo los campos eléctrico y magnético, cuando son variables en el tiempo, constituyen respectivamente fuentes de campo magnético y eléctrico, respectivamente.
- Campos magnéticos dependientes del tiempo
- Campos eléctricos dependientes del tiempo
- Las ecuaciones de Maxwell
(continúa hacia abajo)
👇
Campos magnéticos dependientes del tiempo
Al tratar los fenómenos de inducción, hemos visto que cuando se tiene un campo $\vec B$ variable que atraviesa un circuito, da lugar en él a una fem inducida, de acuerdo a la ley de Faraday-Henry:
$$ \mathcal{E} = -\frac{\mathrm d\symup\Phi}{\mathrm d t} = -\frac{\mathrm d}{\mathrm d t}\int_S \vec B\cdot \mathrm d \vec S $$La presencia de la fem inducida implica que existe un campo eléctrico $\vec E$ tal que:
$$ \mathcal{E} = \oint_\ell \vec E\cdot \mathrm d \vec \ell $$Igualando ambas expresiones:
$$ \oint_\ell \vec E\cdot \mathrm d \vec \ell = -\frac{\mathrm d}{\mathrm d t}\int_S \vec B\cdot \mathrm d \vec S $$Esta es la expresión integral de la ley de Faraday-Henry que, como veremos, constituye la tercera ecuación de Maxwell.
Dicha ley puede expresarse en forma diferencial, de modo que:
$$ \nabla\times\vec E = -\frac{\partial \vec B}{\partial t} $$Así, todo campo magnético variable con el tiempo constituye una fuente de campo eléctrico. A diferencia de las cargas eléctricas, el campo variable es una fuente vectorial (módulo, dirección y sentido).
De la anterior ecuación se deduce además que el campo eléctrico generado es no conservativo, puesto que su rotacional es distinto de cero.
Campos eléctricos dependientes del tiempo
La íntima relación entre los campos eléctrico y magnético sugiere que debería existir una expresión análoga en la que la variación de un campo eléctrico genere un campo magnético.
Se sabe que la circulación del campo magnético viene dada por la ley de Ampère:
$$ \oint \vec B\cdot \mathrm d \vec \ell = \mu \int_S \vec J\cdot \mathrm d \vec S $$Sin embargo, esta expresión no contiene ningún campo eléctrico variable, puesto que se ha obtenido en condiciones estacionarias.
En el caso de considerar un campo eléctrico variable, la ley de Ampère debe corregirse, de forma que:
$$ \oint \vec B\cdot \mathrm d \vec \ell = \mu \int_S \vec J\cdot \mathrm d \vec S + \mu\varepsilon\frac{\mathrm d}{\mathrm d t}\int_S \vec E\cdot \mathrm d \vec S, $$expresión que se conoce como ley de Ampère-Maxwell (en su forma integral), ya que fue James Clerk Maxwell quien primero introdujo esta modificación, más por compatibilidad matemática que por los resultados experimentales.
Aprende más sobre James Clerk Maxwell echando un vistazo a su biografía científica en nuestra sección de Historia de la Ciencia.
En su forma diferencial, viene dada por:
$$ \nabla\times\vec B = \mu\left(\vec J + \varepsilon\frac{\partial \vec E}{\partial t}\right) $$Así, el campo magnético tiene dos fuentes, las corrientes, caracterizadas por $\vec J$, y las variaciones del campo eléctrico, cuyo efecto es añadir un término a la densidad de corriente $\vec J$.
Maxwell interpretó este término como una corriente adicional a la que denominó corriente de desplazamiento.
Las ecuaciones de Maxwell
Maxwell encontró que las leyes experimentales de la electricidad y el magnetismo podían resumirse en un grupo de ecuaciones, que en la actualidad se conocen como las ecuaciones de Maxwell.
Estas ecuaciones relacionan el campo eléctrico $\vec E$ y el campo magnético $\vec B$ con sus fuentes, como son las cargas eléctricas, las corrientes y los campos variables.
A partir de estas ecuaciones pueden deducirse todas las leyes del electromagnetismo (Coulomb, Gauss, Biot y Savart y Ampère).
A continuación se expresan las cuatro leyes de Maxwell en su forma integral y diferencial:
- La primera ecuación relaciona el campo eléctrico con sus fuentes escalares, que son las cargás eléctricas caracterizadas por $\rho$ (densidad de carga).
- La segunda ecuación indica que el campo magnético no tiene fuentes escalares, y por eso su divergencia es nula.
- La tercera ecuación relaciona el campo eléctrico con sus fuentes vectoriales, que son los campos magnéticos variables en el tiempo.
- La cuarta ecuación relaciona el campo magnético con sus fuentes vectoriales, que son tanto las corrientes eléctricas, caracterizadas por la densidad de corriente J, como los campos eléctricos variables en el tiempo, que se interpretan como corrientes de desplazamiento.
Estas ecuaciones juegan en el electromagnetismo clásico un papel semejante a las leyes de Newton en la mecánica clásica, aunque se trata de ecuaciones considerablemente más complicadas y su aplicación en la resolución de problemas requiere un conocimiento matemático muy superior.
Exportar a PDF
📥 Pincha aquí y sigue estas instrucciones:
- Abre el diálogo de Impresión (Control-P si estás en Windows).
- Cambia el Destino a Guardar como PDF.
- Cambia el Diseño a Horizontal.
- Cambia los Márgenes a Ninguno.
- Activa la opción Gráficos de fondo.
El proceso, en principio, solo funciona con Google Chrome.