Campo magnético

Introducción
Ley de Biot y Savart
Ley de Ampère
Ley de Lorentz
Dispositivos
Ley de Laplace

Descarga estas diapositivas en formato PDF 📥

El campo magnético es una perturbación en el espacio producida por la presencia de corrientes eléctricas. Se trata de una magnitud vectorial definida en cada punto del espacio perturbado. Se denota por $\vec B$ y su unidad en el SI es el tesla (T), equivalente a V s/m².

El tesla es una unidad muy grande, por lo que en ocasiones se utiliza también el gauss (G), cuya equivalencia es: 1 T = 10⁴ G.

Introducción

Pierre de Maricourt
El descubrimiento de la brújula
Experiencias de Ørsted y de Faraday-Henry
Magnetismo

(continúa hacia abajo)

👇

Los imanes naturales eran ya conocidos en la Antigua Grecia. Se sabía que algunos minerales como la magnetita tenían la propiedad de atraer piezas de hierro.

Magnetita de Bolivia. [© Rob Lavinsky & iRocks.com](https://commons.wikimedia.org/wiki/File:Magnetite-118736.jpg). — Magnetita de Bolivia. © Rob Lavinsky & iRocks.com.

Durante mucho tiempo, el estudio del magnetismo se limitó a estudiar estos imanes naturales.

Pierre de Maricourt

En 1269, Pierre de Maricourt observó que todos los imanes, independientemente de su forma, poseían dos polos (N y S) en los que la fuerza ejercida por el imán presentaba su máxima intensidad.

Descubrió además que al aproximar polos iguales se repelían. Por el contrario, si se aproximaban polos opuestos se atraían.

Observó también que los polos nunca se encuentran aislados.

Si se parte un imán en dos trozos, se obtienen dos nuevos imanes, ambos con sus dos polos N y S (diferencia esencial con las cargas eléctricas).

El descubrimiento de la brújula

El descubrimiento de todos estos fenómenos magnéticos hizo posible el desarrollo de la brújula, que se atribuye a los chinos en el s. XI, aunque en Europa no comenzó a utilizarse hasta el s. XII.

Maqueta de un cucharón o *sinan* de la [dinastía Han](https://es.wikipedia.org/wiki/Dinastía_Han) (206 a.C. – 220 d.C.) hecho de [piedras de imán](https://es.wikipedia.org/wiki/Piedra_de_imán). — Maqueta de un cucharón o *sinan* de la dinastía Han (206 a.C. – 220 d.C.) hecho de piedras de imán.

En 1600, el inglés William Gilbert, científico y médico de la Reina Isabel I de Inglaterra, explicó el comportamiento de las brújulas suponiendo que la Tierra era un gigantesco imán con el polo Sur magnético en el polo Norte geográfico.

[**Campo magnético terrestre**](https://es.wikipedia.org/wiki/Campo_magnético_terrestre), aproximado con el campo creado por un [dipolo magnético](https://es.wikipedia.org/wiki/Dipolo_magnético) (un imán de barra), donde se observan las líneas de campo magnético (siempre cerradas), saliendo del polo norte y entrando por el polo sur. — **Campo magnético terrestre**, aproximado con el campo creado por un dipolo magnético (un imán de barra), donde se observan las líneas de campo magnético (siempre cerradas), saliendo del polo norte y entrando por el polo sur.

Los polos magnéticos de la Tierra no coinciden exactamente con los geográficos. Entre ellos existe un ángulo denominado declinación magnética que varía en el tiempo y en el espacio.

Origen del campo magnético terrestre

La hipótesis de la dinamo es una teoría científica que intenta explicar el mecanismo por el que un cuerpo celeste, como por ejemplo la Tierra, genera un campo magnético a su alrededor.

En el caso de la Tierra, se cree que su campo magnético está causado por el movimiento de convección del hierro y níquel fundidos en el interior del núcleo terrestre exterior, así como el efecto Coriolis que aparece por la rotación del planeta.

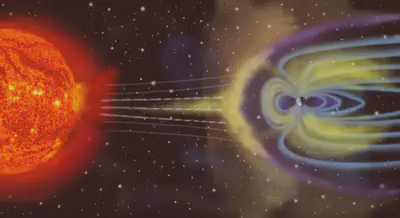
El campo magnético terrestre interacciona con el viento solar en una región que se conoce como la magnetosfera, que se extiende desde los 500 km de altura hasta miles de kilómetros en el espacio. Esta interacción es la principal causa de las auroras polares.

Representación artística de la magnetosfera terrestre.

Aprende más sobre imanes y brújulas con esta excelente simulación:

Experiencias de Ørsted y de Faraday-Henry

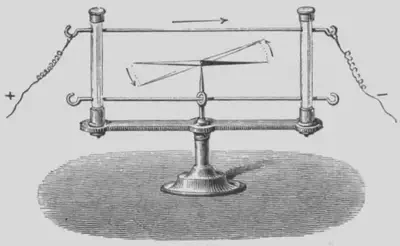
Los fenómenos eléctricos y magnéticos están íntimamente relacionados, pero la conexión entre ambos no se hizo hasta comienzos del s. XIX, cuando Ørsted descubrió que las corrientes eléctricas eran capaces de influir sobre la aguja de una brújula, modificando el magnetismo.

Pocos años después, Faraday y Henry observaron el efecto contrario. Al acercar o alejar un imán a un conductor, se generaba en él una corriente eléctrica.

Puedes aprender más jugando con esta simulación:

Todos estos hechos pusieron de manifiesto la íntima relación entre la electricidad y el magnetismo.

Magnetismo

Posteriormente, Ampère sentó las bases del magnetismo, proponiendo un modelo según el cual las fuentes del campo magnético no son los imanes, sino las corrientes eléctricas.

Según su teoría, el magnetismo de los imanes se debe a la existencia de pequeñas corrientes eléctricas a escala atómica, debidas al movimiento de electrones.

Estas corrientes están orientadas de forma que sus efectos se suman (ferromagnetismo) o se cancelan (diamagnetismo) (en los materiales paramagnéticos los dipolos solo se alinean si existe un campo externo).

Hoy sabemos que el magnetismo de los imanes es debido principalmente al momento magnético de espín de los electrones, además de su propio movimiento como postuló Ampère.

Ley de Biot y Savart

El campo magnético $\vec B$ generado por una corriente $I$ viene dado por la ley de Biot y Savart:

$$ \mathrm d \vec B = \frac{\mu}{4\pi}\frac{I\mathrm d \vec \ell \times \hat{\mathrm r}}{r^2}, $$

donde $\mu$ es la permeabilidad magnética ($\approx 4\pi\times 10^{-7}\,\mathrm{N\,A^{-2}}$ en el vacío), $r$ es la distancia del elemento de corriente $\mathrm d \vec \ell$ al punto P y $\hat{\mathrm r}$ es el vector unitario desde el elemento $\mathrm d \vec \ell$ hacia P.

De acuerdo con la expresión anterior, el $\mathrm d \vec B$ generado:

Módulo: $\displaystyle \mathrm d B = \frac{\mu}{4\pi}\frac{I\mathrm d \ell \sin\theta}{r^2}$, siendo $\theta$ el ángulo formado entre $\mathrm d \vec \ell$ y $\hat{\mathrm r}$
Dirección: $\perp$ al plano formado por $\mathrm d \vec \ell$ y $\hat{\mathrm r}$
Sentido: regla de la mano derecha o regla del sacacorchos.

¿Cómo indicamos si un vector entra o sale del papel?

Las notaciones utilizadas para indicar que un vector entra (izquierda) o sale (derecha) de la pantalla o de una página.

Si integramos la ley de Biot y Savart a la corriente completa, se obtiene el campo magnético total en el punto P.

Vamos a aplicarlo a dos casos concretos:

Campo creado por un hilo conductor infinito
Campo creado por una espira de corriente en su eje

(continúa hacia abajo)

👇

Campo creado por un hilo conductor infinito

De acuerdo a la ley de Biot y Savart:

$$ \mathrm d B = \frac{\mu}{4\pi}\frac{I\mathrm d \ell \sin\theta}{r^2} $$

Para integrar necesitamos expresarlo todo en función de una única variable (en este caso el ángulo $\theta$):

$$ \begin{gathered} R = r\sin\left(\pi-\theta\right) = r\sin\theta \rightarrow r = \frac{R}{\sin\theta}\qquad (1) \\[1ex] \frac{R}{x} = \tan\left(\pi-\theta\right) = -\tan\theta; x = -\frac{R}{\tan\theta}\notag \\[1ex] \mathrm d x = \mathrm d \ell = \frac{R}{\tan^2\theta}\cdot \frac{1}{\cos^2\theta}\,\mathrm d \theta = \frac{R}{\sin^2\theta}\,\mathrm d \theta\qquad (2) \end{gathered} $$

Sustituyendo (1) y (2) se tiene:

$$ \mathrm d B = \frac{\mu I}{4\pi}\frac{R}{\sin^2\theta}\frac{\sin^3\theta}{R^2}\,\mathrm d \theta = \frac{\mu I}{4\pi R}\sin\theta\,\mathrm d \theta $$

Hay que integrar para el hilo completo $\left(x \rightarrow -\infty: \theta = 0; x \rightarrow \infty: \theta = \pi\right)$:

$$ B = \int_{\theta = 0}^{\theta = \pi} \frac{\mu I}{4\pi R}\sin\theta\,\mathrm d \theta = \left. -\frac{\mu I}{4\pi R }\cos\theta \right |_0^\pi = \boxed{\frac{\mu I}{2\pi R}} $$

¿Cómo es el campo creado por dos hilos conductores infinitos?

Consideremos dos casos, siguiendo la notación de esta figura:

Corrientes circulan en el mismo sentido
Corrientes circulan en sentidos opuestos

(continúa hacia abajo)

👇

Corrientes circulan en el mismo sentido

Dado que, en la región entre los dos hilos, los campos creados por cada hilo tienen sentidos opuestos, existe un punto en el que el campo magnético total se anula.

Tomando $y=0$ la posición del hilo 1 (el hilo 2 estaría situado en $y=d$):

$$ \begin{aligned} \vec B_\mathrm t = \vec B_1 + \vec B_2 &= \frac{\mu I_1}{2\pi y}\hat{\mathrm k}-\frac{\mu I_2}{2\pi \left(d-y\right)}\hat{\mathrm k} = \vec 0 \\ &\Updownarrow \\ B_1 &= B_2 \\ \frac{\mu I_1}{2\pi y} &= \frac{\mu I_2}{2\pi \left(d-y\right)} \rightarrow y = \frac{I_1}{I_1+I_2}d \end{aligned} $$

Si $I_1=I_2$, entonces el punto donde el campo magnético total se anula está en el medio de ambos hilos ($y=d/2$).

Corrientes circulan en sentidos opuestos

Puede demostrarse que, en el caso de que las corrientes circulen en sentidos opuestos, el punto donde el campo magnético se anula está fuera del espacio entre los hilos, hacia el exterior del hilo con la corriente menor ($I_2$ en este caso), a una distancia:

$$ y = \frac{I_1}{I_1-I_2}d,\quad\text{con }I_1>I_2 $$

Si $I_1=I_2$, las distancias adicionales hacen que no haya un punto donde los campos se cancelen exactamente debido a la geometría y la distancia involucrada.

Campo creado por una espira de corriente en su eje

Consideremos una espira de radio $R$ por la que circula una corriente $I$ en sentido antihorario.

$$ \begin{gathered} \mathrm d \vec \ell \perp \hat{\mathrm r} \Rightarrow \sin\theta=1 \\ \mathrm d \vec B \perp \hat{\mathrm r}\text{ y }\mathrm d \vec B \perp \mathrm d \vec \ell \\ r^2 = z^2+R^2 \\ \mathrm d B = \frac{\mu}{4\pi}\frac{I\mathrm d \ell}{z^2+R^2} \end{gathered} $$

Por geometría, si se consideran $\mathrm d B_y$ generados por todos los elementos de corriente de la espira, estos se cancelan. Así, solo quedan componentes $\mathrm d B_z$:

$$ \begin{aligned} \mathrm d B_z & = \mathrm d B\cos\phi = \frac{\mu}{4\pi}\frac{I\mathrm d \ell \sin\theta}{z^2+R^2}\frac{R}{\sqrt{z^2+R^2}} = \frac{\mu IR}{4\pi}\frac{\mathrm d \ell}{\left(z^2+R^2\right)^{3/2}} \\ B_z & = \int \mathrm d B_z = \frac{\mu I}{4\pi}\frac{R}{\left(z^2+R^2\right)^{3/2}}\int\mathrm d \ell = \frac{\mu I R^2}{2\left(z^2+R^2\right)^{3/2}} \end{aligned} $$$$ B_z(z=0) = \frac{\mu I}{2R}\quad\text{(campo en el centro de la espira)} $$

Dirección ($\perp$ al plano de la espira) y sentido (regla de la mano derecha) de $\vec B$. Las espiras se comportan como imanes, con su cara norte y su cara sur.

El campo magnético también debe cumplir el principio de superposición. Si en un punto tenemos $\vec B_i$ creados por diferentes corrientes, el campo magnético total, $\vec B_\mathrm t$, viene dado por:

$$ \vec B_\mathrm t = \sum_i \vec B_i $$

Campo magnético generado por agrupaciones de corrientes: ley de Ampère

Para calcular el campo generado por una agrupación de corrientes se emplea la ley de Ampère.

Antes de enunciar esta ley resulta necesario definir la circulación de un campo vectorial $\vec A$:

$$ \oint \vec A\cdot \mathrm d \vec \ell,\quad \text{con $\mathrm d \vec \ell$ tangente a la línea cerrada en cada punto} $$

En los campos conservativos, como $\vec g$ o $\vec E$, esta circulación se hace cero puesto que existe un potencial:

Pero el campo magnético es no conservativo:

No existe un potencial magnético.
El trabajo realizado por la fuerza magnética depende del camino seguido.
La circulación de $\vec B$ es distinta de cero.

La ley de Ampère generaliza este resultado para cualquier agrupación de corrientes:

La circulación de $\vec B$ a lo largo de una línea cerrada es la suma de las intensidades que atraviesan la superficie determinada por dicha línea, multiplicada por la permeabilidad magnética:
$$ \oint \vec B\cdot \mathrm d \vec \ell = \mu \sum_i I_i $$

Campo creado en el interior de un solenoide

Un solenoide o bobina está formado por un hilo de corriente enrollado formando $N$ espiras que se orientan en torno a un eje. El solenoide se comporta, en su conjunto, como un imán:

Según la ley de Ampère:

$$ BL = \mu NI \rightarrow B = \mu NI/L = \mu nI, $$

con $n = N/L$ el número de espiras por unidad de longitud.

Así, el campo magnético generado por un solenoide en su interior:

Es uniforme y su módulo $B = \mu nI$.
Dirección la del eje del solenoide.
Sentido dado por la regla de la mano derecha.

Efecto del campo magnético sobre una carga en movimiento: ley de Lorentz

Cuando una carga puntual $q$ de masa $m$ se desplaza con velocidad $\vec v$ en el interior de un campo magnético uniforme $\vec B$, estará sometida a una fuerza $\vec F_\mathrm m$ debida al campo tal que:

$$ \vec F_\mathrm m = q\vec v \times \vec B\quad \text{LEY DE LORENTZ} $$

Módulo: $F_\mathrm m = qvB\sin\theta$, con $\theta$ el ángulo formado entre $\vec v$ y $\vec B$. Es proporcional a $v$ y $B$, se anula cuando $\vec v \parallel \vec B$ y se hace máxima cuando $\vec v \perp \vec B$.
Dirección: Es perpendicular al plano formado por $\vec v$ y $\vec B$. Al ser $\perp$ a $\vec v$, no puede cambiar su módulo, únicamente la trayectoria de $q$. Al ser también $\perp$ al desplazamiento, tampoco realiza trabajo.
Sentido: Regla de la mano derecha si la carga es positiva.

Conocida $\vec F_\mathrm m$ es posible describir el movimiento de la carga en $\vec B$ (considerado siempre uniforme).

Consideremos tres casos:

Velocidad paralela al campo ($\symbf{\vec v \parallel \vec B}$)
Velocidad perpendicular al campo ($\symbf{\vec v \perp \vec B}$)
Caso general

(continúa hacia abajo)

👇

Velocidad paralela al campo ($\symbf{\vec v \parallel \vec B}$)

Como $\vec v \parallel \vec B$, $\vec F_\mathrm m = 0$, por lo que $q$ describe un MRU.

Velocidad perpendicular al campo ($\symbf{\vec v \perp \vec B}$)

Si $q$ fuera negativa, la trayectoria sería en sentido horario.

Debido a $\vec F_\mathrm m$, la partícula describe un MCU de radio:

$$ \begin{aligned} F_\mathrm m & = ma \\ F_\mathrm m & = ma_\mathrm c = \frac{mv^2}{r} \\ qvB & = \frac{mv^2}{r} \rightarrow r = \frac{mv}{qB} \end{aligned} $$

Cuanto mayor sea $v$ y menor $B$, el radio será mayor. Con $v$ y $B$ constantes, el radio únicamente depende de la relación masa/carga.

El periodo

$$ T = \frac{2\pi r}{v} = \frac{2\pi \dfrac{mv}{qB}}{v} = \frac{2\pi m}{qB} $$

y la frecuencia $f$

$$ f = \frac{1}{T} = \frac{qB}{2\pi m} $$

son independientes de la velocidad y del radio. Se denominan periodo y frecuencia del ciclotrón.

Caso general

La velocidad $\vec v$ puede descomponerse en una componente paralela a $\vec B$, $v_\parallel$, que no se ve afectada por $\vec F_\mathrm m$ y permanece constante, y otra componente perpendicular a $\vec B$, $v_\perp$, que da lugar a un MCU.

Componiendo ambos se observa que $q$ describe un movimiento helicoidal en el que el giro se debe a $v_\perp$ y el avance de la hélice a $v_\parallel$, de forma que el paso de la hélice, $p$, viene dado por:

$$ p = v_\parallel\cdot T = v_\parallel \cdot \frac{2\pi m}{qB} $$

Existen varios dispositivos que aprovechan el movimiento de partículas cargadas dentro de un campo $\vec B$.

(continúa hacia abajo)

👇

Selector de velocidades

Es un dispositivo que permite seleccionar partículas que se mueven a cierta velocidad. En él hay un campo magnético y un campo eléctrico uniformes y perpendiculares entre sí.

Supongamos una carga $q$ positiva que penetra con velocidad $\vec v$ en el selector. Dicha carga se verá sometida a dos fuerzas:

$\vec F_\mathrm m$ debida a $\vec B$. De acuerdo con la regla de la mano derecha, su dirección y sentido serán tal y como se refleja en la figura.
$\vec F_\mathrm e$ debida a $\vec E$. Como la carga es positiva, dicha fuerza tendrá la misma dirección y sentido que $\vec E$.

Las partículas que salen del selector son aquellas que no se desvían, tal que $F_\mathrm m$ y $F_\mathrm e$ se contrarrestan y describen, por tanto, un MRU:

$$ \begin{aligned} F_\mathrm m & = F_\mathrm e \\ qvB & = qE \rightarrow v = \frac{E}{B} \end{aligned} $$

Espectrómetro de masas

Se emplea para determinar la relación masa/carga de iones cuya carga es conocida, midiendo el radio de la trayectoria circular que describen en el seno de un campo magnético uniforme $\vec B$ conocido.

Los iones de carga $q$ conocida son acelerados por la acción de una diferencia de potencial $\symup\Delta V$ y penetran en una región en la que existe $\vec B$ uniforme generado por un electroimán.

Si los iones parten del reposo y alcanzan una velocidad $v$ al entrar en $\vec B$, por conservación de la energía:

$$ q\symup\Delta V = \frac{1}{2}mv^2\rightarrow v = \sqrt{\frac{2q\symup\Delta V}{m}}\qquad (3) $$

Una vez en $\vec B$, la carga $q$ describe una semicircunferencia de radio $r$ hasta incidir sobre una placa fotográfica:

$$ \begin{aligned} F_\mathrm m & = ma \notag \\ F_\mathrm m & = ma_\mathrm c = \frac{mv^2}{r} \notag \\ \label{eq:v2} qvB & = \frac{mv^2}{r} \rightarrow v = \frac{qBr}{m}\qquad (4) \end{aligned} $$

Igualando (3) y (4):

$$ \frac{q}{m} = \frac{2\symup\Delta V}{B^2 r^2} $$

Esto permite separar y cuantificar los isótopos de elementos químicos, como por ejemplo el hidrógeno.

Acelerador de partículas: el ciclotrón

El ciclotrón es un dispositivo capaz de acelerar partículas cargadas hasta conseguir que adquieran altas energías cinéticas.

Después de ser aceleradas, las partículas suelen emplearse para bombardear núcleos, provocando reacciones nucleares que permiten obtener información sobre estos o dando lugar a materiales radiactivos que se emplean por ejemplo en medicina nuclear.

El ciclotrón está formado por dos recipientes metálicos en forma de “D”, dentro de una cámara de vacío y en el interior de un campo magnético uniforme.

Entre las dos “des” se aplica una diferencia de potencial $\symup\Delta V$ que da lugar a un campo eléctrico en el espacio que las separa.

Esta $\symup\Delta V$ se alterna con un periodo $T'$ que coincide con la mitad del periodo del ciclotrón:

$$ T' = \frac{T}{2} = \frac{\pi m}{qB} $$

Cuando emergen del ciclotrón, las partículas han alcanzado $v_\mathrm{máx} = qBR_\mathrm{ciclotrón}/m \gg v_0$ y por tanto una energía cinética mucho mayor, dada por:

$$ E_\mathrm c = \frac{1}{2}mv_\mathrm{máx}^2 = \frac{1}{2}m\left(\frac{qBR_\mathrm{ciclotrón}}{m}\right)^2 = \frac{q^2B^2R_\mathrm{ciclotrón}^2}{2m}, $$

donde $R_\mathrm{ciclotrón}$ es el radio del ciclotrón (radio de la última semicircunferencia descrita en el ciclotrón).

Efecto del campo magnético sobre una corriente: ley de Laplace

Hemos visto que cuando una carga eléctrica puntual penetra en un campo magnético uniforme $\vec B$, experimenta una fuerza $\vec F_\mathrm m$ debida a $\vec B$ dada por la ley de Lorentz.

En este apartado estudiaremos el efecto de $\vec B$ sobre una corriente eléctrica (conjunto de cargas en movimiento).

Si un hilo conductor por el que circula una corriente $I$ se encuentra en el seno de un $\vec B$ uniforme, cada $\mathrm d \vec \ell$ del hilo experimenta una fuerza magnética $\mathrm d \vec F_\mathrm m$ debida a $\vec B$, dada por:

$$ \mathrm d \vec F_\mathrm m = I\mathrm d \vec \ell\times\vec B\quad \text{LEY DE LAPLACE} $$

Si integramos a todo el hilo obtendremos la $\vec F_\mathrm m$ total que se ejerce sobre él.

Lo aplicaremos a dos casos:

Hilo conductor rectilíneo
Espira de corriente

(continúa hacia abajo)

👇

Hilo conductor rectilíneo

$$ \vec F_\mathrm m = I\vec L\times\vec B, $$

donde $\vec L$ es un vector que tiene la misma dirección que el hilo y su sentido es el de la corriente.

Módulo: $F_\mathrm m = ILB\sin\theta$
Dirección: $\perp$ al plano formado por $\vec L$ y $\vec B$
Sentido: Regla de la mano derecha

Acciones entre hilos conductores rectilíneos

Supongamos dos corrientes paralelas entre sí y al eje $x$, separadas una distancia $d$ y por las que circulan sendas corrientes $I_1$ e $I_2$ en el sentido positivo de dicho eje.

La fuerza es atractiva si las corrientes circulan en el mismo sentido, pero repulsiva si circulan en sentidos opuestos.

$I_1$ genera en $I_2$ un $\vec B_1$ saliente:

$$ \vec B_1 = \frac{\mu I_1}{2\pi d}\hat{\mathrm k} $$

Debido a $\vec B_1$, la corriente $I_2$ se ve sometida a una fuerza $\vec F_{12}$:

$$ \vec F_{12} = I_2\vec L\times\vec B_1 = -\frac{\mu I_1 I_2 L}{2\pi d}\hat{\jmath} $$

Haciendo un razonamiento análogo, $I_2$ genera en $I_1$ un $\vec B_2$ entrante:

$$ \vec B_2 = -\frac{\mu I_2}{2\pi d}\hat{\mathrm k} $$

$I_1$ se ve sometida a una fuerza $\vec F_{21}$:

Las corrientes se atraen con una fuerza por unidad de longitud (N/m):

$$ \frac{F}{L} = \frac{\mu I_1 I_2}{2\pi d}, $$

que es mayor cuanto mayores son $I_1$ e $I_2$ y cuanto menor es la distancia $d$ que las separa.

Definición de amperio

Antes de la redefinición de 2019, el amperio se definía a partir de la situación que acabamos de describir:

Un amperio es la intensidad de una corriente constante que, manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de un metro uno del otro, en el vacío, produciría entre esos conductores una fuerza igual a $2\times 10^{-7}\,\mathrm{N/m}$.

Actualmente se define a partir de la carga elemental, de tal forma que un amperio es la corriente eléctrica correspondiente al flujo de $1/(1.602\,176\,634\times 10^{-19}) = 6.241\,509\,074\times 10^{18}$ cargas elementales por segundo.

Exportar a PDF

📥 Pincha aquí y sigue estas instrucciones:

Abre el diálogo de Impresión (Control-P si estás en Windows).
Cambia el Destino a Guardar como PDF.
Cambia el Diseño a Horizontal.
Cambia los Márgenes a Ninguno.
Activa la opción Gráficos de fondo.

El proceso, en principio, solo funciona con Google Chrome.